Hardware Intrinsics in .NET Core

Tanner Gooding [MSFT]

September 3rd, 201935 4

Several years ago, we decided that it was time to support SIMD code in .NET. We introduced the System.Numerics namespace with Vector2, Vector3, Vector4, Vector<T>, and related types. These types expose a general-purpose API for creating, accessing, and operating on them using hardware vector instructions (when available). They also provide a software fallback for when the hardware does not provide the appropriate instructions. This enabled a number of common algorithms to be vectorized, often with only minor refactorings. However, the generality of this approach made it difficult for programs to take full advantage of all vector instructions available on modern hardware. Additionally, modern hardware often exposes a number of specialized non-vector instructions that can dramatically improve performance. In this blog post, I’m exploring how we’ve addressed this limitation in .NET Core 3.0.

What are hardware intrinsics?

In .NET Core 3.0, we added a new feature called hardware intrinsics. Hardware intrinsics provide access to many of these hardware specific instructions that can’t easily be exposed in a more general-purpose mechanism. They differ from the existing SIMD intrinsics in that they are not general-purpose (the new hardware intrinsics are not cross-platform and the architecture does not provide a software fallback) and instead directly expose platform and hardware specific functionality to the .NET developer. The existing SIMD intrinsics, in comparison, are cross-platform, provide a software fallback, and are slightly abstracted from the underlying hardware. That abstraction can come at a cost and prevent certain functionality from being exposed (when said functionality does not exist or is not easily emulated on all target hardware).

The new intrinsics and supporting types are exposed under the System.Runtime.Intrinsics namespace. For .NET Core 3.0 there currently exists one namespace: System.Runtime.Intrinsics.X86. We are working on exposing hardware intrinsics for other platforms, such as System.Runtime.Intrinsics.Arm.

Under the platform specific namespaces, intrinsics are grouped into classes which represent logical hardware instruction groups (frequently referred to as Instruction Set Architectures or ISAs). Each class then exposes an IsSupported property that indicates whether the hardware you are currently executing on supports that instruction set. Each class then also exposes a set of methods that map to the underlying instructions exposed by that instruction set. There is sometimes additionally a subclass that is part of the same instruction set but that may be limited to specific hardware. For example, the Lzcnt class provides access to the leading zero count instructions. There is then a subclass named X64 which exposes the forms of the instruction that are only usable on 64-bit machines.

Some of the classes are also hierarchical in nature. For example, if Lzcnt.X64.IsSupported returns true, then Lzcnt.IsSupported must also return true since it is an explicit subclass. Likewise, if Sse2.IsSupported returns true, then Sse.IsSupported must also return true because Sse2 explicitly inherits from the Sseclass. However, it is worth noting that just because classes have similar names does not mean they are definitely hierarchical. For example, Bmi2 does not inherit from Bmi1 and so the IsSupported checks for the two instruction sets are distinct from each other. The design philosophy of these types is to truthfully represent the ISA specification. SSE2 requires to support SSE1, so we exposed a subclass and since BMI2 doesn’t require supporting BMI1, we didn’t use inheritance.

An example of the API shape described above is the following:

You can also see a more complete list by browsing the source code on source.dot.net or dotnet/coreclr on GitHub.

The IsSupported checks are treated as runtime constants by the JIT (when optimizations are enabled) and so you do not need to cross-compile to support multiple different ISAs, platforms, or architectures. Instead, you just write your code using if-statements and the unused code paths (any code path which is not executed, due to the condition for the branch being false or an earlier branch being taken instead) are dropped from the generated code (the native assembly code generated by the JIT at runtime).

It is essential that you guard usage of hardware intrinsics with the appropriate IsSupported check. If your code is unguarded and runs on a machine or architecture/platform that doesn’t support the intrinsic, a PlatformNotSupportedException is thrown by the runtime.

What benefits do these provide me?

Hardware Intrinsics definitely aren’t for everyone, but they can be used to boost perf in some computationally heavy workloads. Frameworks such as CoreFX or ML.NET take advantage of these methods to help accelerate things like copying memory, searching for the index of an item in an array/string, resizing images, or working with vectors, matrices, and tensors. Manually vectorizing some code that has been identified as a bottleneck can also be easier than it seems. Vectorizing your code is really all about performing multiple operations at once, generally using Single-Instruction Multiple Data (SIMD) instructions.

It is important to profile your code before vectorizing to ensure that the code you are optimizing is part of a hot spot (and therefore the optimization will be impactful). It is also important to profile while you are iterating on the vectorized code, as not all code will benefit from vectorization.

Vectorizing a simple algorithm

Take for example an algorithm which sums all elements in an array or span. This code is a perfect candidate for vectorization because it does the same unconditional operation every iteration of the loop and those operations are fairly trivial in nature.

An example of such an algorithm might look like the following:

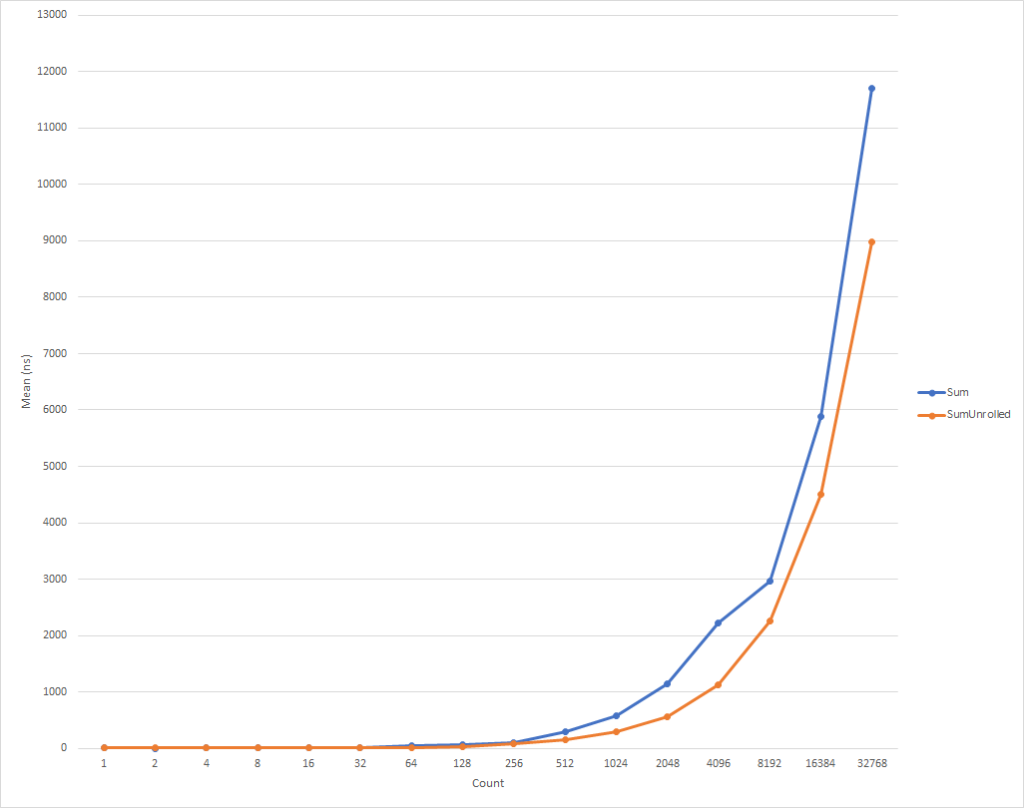
The code is simple and understandable, but it is also not particularly fast for large inputs since you are only doing a single trivial operation per loop iteration.

Method Count Mean Error StdDev
Sum 1 2.477 ns 0.0192 ns 0.0179 ns
Sum 2 2.164 ns 0.0265 ns 0.0235 ns
Sum 4 3.224 ns 0.0302 ns 0.0267 ns
Sum 8 4.347 ns 0.0665 ns 0.0622 ns
Sum 16 8.444 ns 0.2042 ns 0.3734 ns
Sum 32 13.963 ns 0.2182 ns 0.2041 ns
Sum 64 50.374 ns 0.2955 ns 0.2620 ns
Sum 128 60.139 ns 0.3890 ns 0.3639 ns
Sum 256 106.416 ns 0.6404 ns 0.5990 ns
Sum 512 291.450 ns 3.5148 ns 3.2878 ns
Sum 1024 574.243 ns 9.5851 ns 8.4970 ns
Sum 2048 1,137.819 ns 5.9363 ns 5.5529 ns
Sum 4096 2,228.341 ns 22.8882 ns 21.4097 ns
Sum 8192 2,973.040 ns 14.2863 ns 12.6644 ns
Sum 16384 5,883.504 ns 15.9619 ns 14.9308 ns
Sum 32768 11,699.237 ns 104.0970 ns 97.3724 ns

Improving the perf by unrolling the loop

Modern CPUs have many ways of increasing the throughput at which it executes your code. For single-threaded applications, one of the ways it can do this is by executing multiple primitive operations in a single cycle (a cycle is the basic unit of time in a CPU).

Most modern CPUs can execute about 4 add operations in a single cycle (under optimal conditions), so by laying out your code correctly and profiling it, you can sometimes optimize your code to have better performance, even when only executing on a single-thread.

While the JIT can perform loop unrolling itself, it is conservative in deciding when to do so due to the larger codegen it produces. So, it can be beneficial to manually unroll the loop in your source code instead.

You might unroll your code like the following:

The code is slightly more complicated but takes better advantage of your hardware.

For really small loops, the code ends up being slightly slower, but that normalizes itself for inputs that have 8 elements and then starts getting faster for inputs with even more elements (taking 26% less time at 32k elements). It’s also worth noting that this optimization doesn’t always improve performance. For example, when handling float, the unrolled version is practically the same speed as the original version, so it’s important to profile your code accordingly.

Method Count Mean Error StdDev
SumUnrolled 1 2.922 ns 0.0651 ns 0.0609 ns
SumUnrolled 2 3.576 ns 0.0116 ns 0.0109 ns
SumUnrolled 4 3.708 ns 0.0157 ns 0.0139 ns
SumUnrolled 8 4.832 ns 0.0486 ns 0.0454 ns
SumUnrolled 16 7.490 ns 0.1131 ns 0.1058 ns
SumUnrolled 32 11.277 ns 0.0910 ns 0.0851 ns
SumUnrolled 64 19.761 ns 0.2016 ns 0.1885 ns
SumUnrolled 128 36.639 ns 0.3043 ns 0.2847 ns
SumUnrolled 256 77.969 ns 0.8409 ns 0.7866 ns
SumUnrolled 512 146.357 ns 1.3209 ns 1.2356 ns
SumUnrolled 1024 287.354 ns 0.9223 ns 0.8627 ns
SumUnrolled 2048 566.405 ns 4.0155 ns 3.5596 ns
SumUnrolled 4096 1,131.016 ns 7.3601 ns 6.5246 ns
SumUnrolled 8192 2,259.836 ns 8.6539 ns 8.0949 ns
SumUnrolled 16384 4,501.295 ns 6.4186 ns 6.0040 ns
SumUnrolled 32768 8,979.690 ns 19.5265 ns 18.2651 ns

Improving the perf by vectorizing the loop

However, we can still optimize the code a bit more. SIMD instructions are another way modern CPUs allow you to improve throughput. Using a single instruction they allow you to perform multiple operations in a single cycle. This can be better than the loop unrolling because it performs essentially the same operation, but with smaller generated code.

To elaborate a bit, each one of the add instructions from the unrolled loop is 4 bytes in size, so it takes 16-bytes of space to have all 4 adds in the unrolled form. However, the SIMD add instruction also performs 4 additions, but it only takes 4 bytes to encode. This means there are less instructions for the CPU to decode and execute each iteration of the loop. There are also other things the CPU can assume and optimize around for this single instruction, but those are out of scope for this blog post. What’s even better is that modern CPUs can also execute more than one SIMD instruction per cycle, so in certain cases you can then unroll your vectorized code to improve the performance further.

You should generally start by looking at whether the general-purpose Vector<T> class will suit your needs. It, like the newer hardware intrinsics, will emit SIMD instructions, but given that it is general-purpose you can reduce the amount of code you need to write/maintain.

The code might look like:

The code is faster, but we have to fall back to accessing individual elements when computing the overall sum. Vector<T> also does not have a well-defined size and can vary based on the hardware you are running against. The hardware intrinsics provide some additional functionality that can make this code a bit nicer and faster still (at the cost of additional code complexity and maintainence requirements).

Method Count Mean Error StdDev
SumVectorT 1 4.517 ns 0.0752 ns 0.0703 ns
SumVectorT 2 4.853 ns 0.0609 ns 0.0570 ns
SumVectorT 4 5.047 ns 0.0909 ns 0.0850 ns
SumVectorT 8 5.671 ns 0.0251 ns 0.0223 ns
SumVectorT 16 6.579 ns 0.0330 ns 0.0276 ns
SumVectorT 32 10.460 ns 0.0241 ns 0.0226 ns
SumVectorT 64 17.148 ns 0.0407 ns 0.0381 ns
SumVectorT 128 23.239 ns 0.0853 ns 0.0756 ns
SumVectorT 256 62.146 ns 0.8319 ns 0.7782 ns
SumVectorT 512 114.863 ns 0.4175 ns 0.3906 ns
SumVectorT 1024 172.129 ns 1.8673 ns 1.7467 ns
SumVectorT 2048 429.722 ns 1.0461 ns 0.9786 ns
SumVectorT 4096 654.209 ns 3.6215 ns 3.0241 ns
SumVectorT 8192 1,675.046 ns 14.5231 ns 13.5849 ns
SumVectorT 16384 2,514.778 ns 5.3369 ns 4.9921 ns
SumVectorT 32768 6,689.829 ns 13.9947 ns 13.0906 ns

NOTE: For the purposes of this blogpost, I forced the size of Vector<T> to 16-bytes using an internal configuration knob (COMPlus_SIMD16ByteOnly=1). This normalized the results when comparing SumVectorT to SumVectorizedSse and kept the latter code simpler. Namely, it avoided the need to write an if (Avx2.IsSupported) { } code path. Such a code path is nearly identical to the Sse2 path, but deals with Vector256<T> (32-bytes) and processes even more elements per loop iteration.

So, you might take advantage of the new hardware intrinsics like so:

The code is again slightly more complicated, but it’s significantly faster for all but the smallest workloads. At 32k elements, it’s taking 75% less time than the unrolled loop and 81% less than the original code.

You’ll notice that we have a few IsSupported checks. The first checks if the hardware intrinsics are supported for the current platform at all and falls back to the unrolled loop if they aren’t. This path will currently be hit for platforms like ARM/ARM64 which don’t have hardware intrinsics or if someone disables them for any reason. The second IsSupported check is in the SumVectorizedSse method and is used to produce slightly better codegen on newer hardware that additionally supports the Ssse3 instruction set.

Otherwise, most of the logic is essentially the same as what we had done for the unrolled version. Vector128<T> is a 128-bit type that contains Vector128<T>.Count elements. In the case of uint, which is itself 32-bits, you have 4 (128 / 32) elements, which is exactly how much we unrolled the loop by.

Method Count Mean Error StdDev
SumVectorized 1 4.555 ns 0.0192 ns 0.0179 ns
SumVectorized 2 4.848 ns 0.0147 ns 0.0137 ns
SumVectorized 4 5.381 ns 0.0210 ns 0.0186 ns
SumVectorized 8 4.838 ns 0.0209 ns 0.0186 ns
SumVectorized 16 5.107 ns 0.0175 ns 0.0146 ns
SumVectorized 32 5.646 ns 0.0230 ns 0.0204 ns
SumVectorized 64 6.763 ns 0.0338 ns 0.0316 ns
SumVectorized 128 9.308 ns 0.1041 ns 0.0870 ns
SumVectorized 256 15.634 ns 0.0927 ns 0.0821 ns
SumVectorized 512 34.706 ns 0.2851 ns 0.2381 ns
SumVectorized 1024 68.110 ns 0.4016 ns 0.3756 ns
SumVectorized 2048 136.533 ns 1.3104 ns 1.2257 ns
SumVectorized 4096 277.930 ns 0.5913 ns 0.5531 ns
SumVectorized 8192 554.720 ns 3.5133 ns 3.2864 ns
SumVectorized 16384 1,110.730 ns 3.3043 ns 3.0909 ns
SumVectorized 32768 2,200.996 ns 21.0538 ns 19.6938 ns

Summary

The new hardware intrinsics allow you to take advantage of platform-specific functionality for the machine you’re running on. There are approximately 1,500 APIs for x86 and x64 spread across 15 instruction sets and far too many to cover in a single blog post. By profiling your code to identify hot spots you can also potentially identify areas of your code that would benefit from vectorization and see some pretty good performance gains. There are multiple scenarios where vectorization can be applied and loop unrolling is just the beginning.

Anyone wanting to see more examples can search for uses of the intrinsics in the framework (see the dotnet and aspnet organizations) or in various other blog posts written by the community. And while the currently exposed intrinsics are extensive, there is still a lot of functionality that could be exposed. If you have functionality you would like exposed, feel free to log an API request against dotnet/corefx on GitHub. The API review process is detailed here and there is a good example for the API Request template listed under Step 1.

Special Thanks

A special thanks to our community members Fei Peng (@fiigii) and Jacek Blaszczynski (@4creators) who helped implement the hardware intrinsics. Also to all the community members who have provided valuable feedback to the design, implementation, and usability of the feature.

Tanner Gooding [MSFT] Software Engineer, .NET Team

Read next

35 comments

Discussion is closed. Login to edit/delete existing comments.

  • Karsten Thamm 0

    How about Matrices ?
    Matrix multiplication and inversion is really intensive (especially from 4X4 and higher).

    I’ve once done it in C++ for 3DNow! (RIP), so the order of operations is essential for performance.

    SSE is ideal for Matrices, Vectors and FFT, especially for mult and invert operations.
    On the other hand, for lager operations the GPU becomes the better solution.

    Inversion can be performed via Cramer for 4X4 and below, but should be implemented in Gauss for higher dimensions. Cramer can benefit from Intrinsics, but it’s hard for Gauss.

    I’m currently using a self implemented Gauss for matrix inversion (self implemented because I rather need numerical stability than performance, ‘cos it’s only performed once per session), but however, for mx inversion intenxive calculations hw acceleration (SSE or GPU) would be a helpful feature.

  • Chris Moore 0

    Hi Tanner,

    I’ve noticed some very odd code generation from some of the intrinsic API’s; for example, the code below was emitted for the Permute4x64 function as invoked from a simple wrapper:

    ; function: Vector256 perm_256x64i(Vector256 ymm0, byte imm8)
    0000h push rsi
    0001h sub rsp,50h
    0005h vzeroupper
    0008h mov rsi,rcx
    000bh vmovupd ymm0,[rdx]
    000fh mov rcx,rsi
    0012h vmovupd [rsp+20h],ymm0
    0018h lea rdx,[rsp+20h]
    001dh movzx r8d,r8b
    0021h call 7FFC7C09A120h
    0026h mov rax,rsi
    0029h vzeroupper
    002ch add rsp,50h
    0030h pop rsi
    0031h ret

    The amount of memory shuffling is really disturbing, but most disturbing as that the intrinsic instruction itself (VPERMQ) is never invoked (or maybe it is invoked by the far call???)

    Any idea what’s going on here?

    • Chris Moore 0

      This issue is apparently happening with a large number of intrinsic functions, including both shuffle and blend intrinsics. In fact, wherever a byte mask is used to control memory movement, code similar to the above is generated and the intrinsic itself never gets invoked. IMO, C#/.Net has always had a dysfunctional approach to any integer type less than 32-bits. Is the problem I’m noticing with the intrinsic code generation somehow related to this situation?

      As it stands, any intrinsic function where memory movement is controlled by a single byte mask is not really usable from a performance perspective! I haven’t gone through them all, but I have yet to find a counterexample. On the other hand, permutations/shuffles controlled by a vector, of bytes or otherwise, seem to be fine.

      Here is one more example. The code generated for vpblendvb is as expected:
      ; function: Vector128 vpblendvb(Vector128 xmm0, Vector128 xmm1, Vector128 xmm2)
      0000h vzeroupper
      0003h xchg ax,ax
      0005h vmovupd xmm0,[rdx]
      0009h vmovupd xmm1,[r9]
      000eh vpblendvb xmm0,xmm0,[r8],xmm1
      0014h vmovupd [rcx],xmm0
      0018h mov rax,rcx
      001bh ret

      Now, here is the code generated for vpblendw predicated on a byte immediate:

      ; function: Vector128 vpblendw(Vector128 xmm0, Vector128 xmm1, byte imm8)
      0000h push rsi
      0001h sub rsp,40h
      0005h vzeroupper
      0008h mov rsi,rcx
      000bh vmovupd xmm0,[rdx]
      000fh vmovupd xmm1,[r8]
      0014h mov rcx,rsi
      0017h vmovapd [rsp+30h],xmm0
      001dh vmovapd [rsp+20h],xmm1
      0023h lea rdx,[rsp+30h]
      0028h lea r8,[rsp+20h]
      002dh movzx r9d,r9b
      0031h call 7FFC89589570h
      0036h mov rax,rsi
      0039h add rsp,40h
      003dh pop rsi
      003eh ret

      • Tanner Gooding Microsoft employee 0

        There are a few existing issues tracking this, for example:
        * https://github.com/dotnet/coreclr/issues/17108
        * https://github.com/dotnet/coreclr/issues/19888
        * https://github.com/dotnet/coreclr/issues/20106

        Basically, the JIT needs to support hardware intrinsics for both direct and indirect invocation. This ensures that hardware intrinsics can be used via reflection, in the immediate window/debugger, or with non-constant inputs.

        The JIT is currently only doing the check on if the input is a constant during IL importation and so it can miss certain values that will eventually be constant such as simple method wrappers or other constant folding done later in the compilation.

        The fix is for the JIT to delay the decision of whether to emit the direct instruction or the fallback method call until later in the compilation (likely in the lowering phase) so that it can currently handle these cases.

        This issue will repro for anything where the instruction requires a constant input, but the workaround is generally to just remove the helper method and invoke it directly instead.

        • Chris Moore 0

          As an end-user of the API, how can I take advantage of this workaround? Would I have to change the code in the Core CLR (which code, specifically?) and make a custom build of the CLR?

          Thanks,
          Chris

          • Tanner Gooding Microsoft employee 0

            The workaround is to just not create wrapper methods around the primitive types for right now. The actual fix is more involved and requires changes to the JIT itself. It is being tracked and prioritized as appropriate based on customer need/feedback.

  • Abhijeet Sarkar 0

    How does all this play with Azure VMs? Will we still be able to make use of intrinsics on a VM that uses vCPUs?

    • Tanner Gooding Microsoft employee 0

      The intrinsics will work on VMs as well. You should consult Azure for details on what CPUs particular virtual machine series use and therefore which instruction sets should be available.

  • David Piepgrass 0

    This is disappointing. I much prefer to write portable code, and I hope Vector<T> will be enhanced in the future with some of the intrinsics offered here. At present, it’s amazing how little it can do.

    • Tanner Gooding Microsoft employee 0

      We are open to API proposals or feature requests which can be logged against dotnet/runtime on GitHub. The hardware intrinsic APIs are meant to fill the gap where there is something that can’t be or isn’t yet exposed in the more portable APIs.

      There is a limit to what Vector can expose specifically because it is general purpose. Not all processors support the same instructions or expose them in the same manner/behavior, so what can be done in a consistent cross-platform manner while still providing performance can be tricky. This is true for just x86/x64 but becomes more apparent when you also consider ARM, ARM64, or one of the many targets supported by other runtimes such as Mono.

  • Ian Marteens 0

    Slightly off-topic: is this code from the post ok?

                vresult = Ssse3.HorizontalAdd(vresult, vresult);
            vresult = Ssse3.HorizontalAdd(vresult, vresult);

    Are two consecutive calls to HorizontalAdd supposed to sum all items in the vector? I’m trying this, but it keeps returning 6 instead of 10:

                    fixed (double* p = stackalloc double[] { 1.0, 2.0, 3.0, 4.0 })
                {
                    v = Avx.LoadVector256(p);
                    v = Avx.HorizontalAdd(v, v);
                    v = Avx.HorizontalAdd(v, v);
                    Console.WriteLine(v.ToScalar());
                }

    (yes, I know I’m using Avx and double precision values, but I thought it would work the same; the Shuffle thing works fine for me)

    • Ian Marteens 0

      … the first HorizontalAdd call converts {1,2,3,4} into {3,3,7,7}, but the second one returns {6,6,14,14}.

      • Tanner Gooding Microsoft employee 0

        Most of the Vector256<T> operations don’t operate as if it was a single contiguous 256-bit buffer. Instead it operates as if it was 2×128-bit buffers.

        This is why it is summing ((3, 3), (7, 7)) rather than (3, 3, 7, 7).

        You can do this a few ways, such as:

        v = Avx.LoadVector256(p);
v = Avx.HorizontalAdd(v, v);
v = Avx.HorizontalAdd(v, v);
Sse.Add(v.GetLower(), v.GetUpper()).ToScalar();

        -or-

        v = Avx.LoadVector256(p);
v = Avx.HorizontalAdd(v, v);
v = Avx2.Permute4x64(v, 0b00_10_01_11);
Avx.HorizontalAdd(v, v).ToScalar();
        • Ian Marteens 0

          Got it! Nice trick, thank you.

  • Karim Sultan 0

    Hi Tanner, Good work to you and your team. After having vectorized some C++ code to do fractal calculations, I wanted to create a C# version and found myself making C DLLs to do this … painfully… but then I found this article, breathed a sigh of relief and said “Oh, thank God”. Really good to see this development, and I may be a year late to the party, but I’m grateful you guys put this support in. Thanks.

Feedback usabilla icon