Developing an app with the Visual Studio 3D Starter Kit, part 2 of 3
A few days ago we talked about how to use the Visual Studio 3D Starter Kit to create a simple dice rolling app. Now we’re going to take the app one step further, by adding some animation. If you need to catch up, here’s a link to the previous blog post.
Let it roll, baby, roll
In order to make anything move in a graphics application, the steps are always the same:
- Set some state (e.g. a Boolean flag) to indicate that an animation should be running. This is also a good time to save the starting position and time of the animation if needed.
- In the Update method (called on every frame before rendering), calculate the object’s position/rotation/scaling (in 3D speak, transforms) using the time between the beginning of the animation and the current frame time. You must also make sure that when the animation ends the state is correctly updated to stop the animation.
- In the Render method, make sure that the transforms are correctly applied to each object.
In our case we will add a new method called RollDie() that will set the state and save the starting time. We will use this method to calculate each die roll result, but for now let’s just execute an animation that rotates the die from 1 to 6.
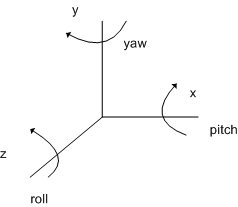
To create this animation we will need a set of variables to keep track of the cube’s transforms, as well as the animation time. We will create one Boolean value to signal that animation is running, one float to store the animation time, and three vectors to store the initial, final and current rotations of the cube. These vectors should be of type XMFLOAT3, to store the Yaw, Pitch and Roll rotations (see figure below).
So let’s create these fields and the RollDie() method. Add the following code to Game.h:
ref class Game sealed : public GameBase { // (snip) other class declarations... Platform::String^ OnHitObject(int x, int y); void RollDie();
private: std::vector<VSD3DStarter::Mesh*> m_meshModels;
bool m_isAnimationRunning;
float m_animationTime;
DirectX::XMFLOAT3 m_initialRotation;
DirectX::XMFLOAT3 m_currentRotation;
DirectX::XMFLOAT3 m_targetRotation;
};
Now, let’s create the animation, beginning with the RollDie() implementation. Add the following code to Game.cpp:
void Game::RollDie()
{
m_initialRotation = m_currentRotation;
m_targetRotation = XMFLOAT3(0.0f, XM_PI, 0.0f); // always rotate to 6
m_animationTime = 0.0f;
m_isAnimationRunning = true;
}
RollDie() will start the animation by setting the m_isAnimationRunning variable to true. We need to add some code to the Update() method to rotate the cube at every frame. The code looks like this:
void Game::Update(float timeTotal, float timeDelta) { if (m_isAnimationRunning)
{
m_animationTime += timeDelta;
static const float animationDuration = 0.5f;
float animationProgress = std::min<float>(m_animationTime / animationDuration, 1.0f);
XMVECTOR initial = XMLoadFloat3(&m_initialRotation);
XMVECTOR target = XMLoadFloat3(&m_targetRotation);
XMVECTOR current = initial + animationProgress * (target - initial);
XMStoreFloat3(&m_currentRotation, current);
if (animationProgress >= 1.0f)
m_isAnimationRunning = false;
}
}
Breaking this code down:
- The animation should only execute if the m_isAnimationRunning flag is set.
- First calculate m_animationTime, the time since the animation started (from 0 to 0.5 seconds) and m_animationProgress, the percentage of the animation that is already done (from 0 to 1). Note that the progress is clamped to 1.0.
- Load the initial and target rotation vectors into XMVECTORs, which enable faster calculation through the use of CPU intrinsics.
- Execute the calculation with a linear formula:
current = initial + progress * (target – initial)
- Store the final calculated value back in m_currentRotation.
- Check if the animation is done and stop it if needed.
The next step in our animation is to use the calculated rotation in the Render method to rotate the cube. To do that, change the following line of code in the Render() method:
void Game::Render() { GameBase::Render();
// (snip) clear...
XMMATRIX transform = XMMatrixRotationRollPitchYawFromVector(XMLoadFloat3(&m_currentRotation));
for (UINT i = 0; i < m_meshModels.size(); i++) { m_meshModels[i]->Render(m_graphics, transform); }
// (snip) MSAA... }
The method we are calling gets a XMVECTOR containing the roll, pitch and yaw and returns a rotation matrix that corresponds to the combined transform. If you prefer, you can also use the XMMatrixRotationRollPitchYaw method which takes the roll, pitch and yaw components separately. You can even use methods to calculate each component and then multiply them yourself – for the full list of methods to generate transform matrices check this MSDN documentation page.
All we need to do now is call the RollDie() method. Let’s call it whenever the user taps or clicks the screen. Add this code to the DirectXPage.xaml.cpp file, in the DirectXPage::OnTapped method:
void DirectXPage::OnTapped(Platform::Object^ sender, TappedRoutedEventArgs^ e) { m_renderer->RollDie();
}
If you run the app now and click/tap anywhere, the dice will roll from 1 to 6!
The app logic: a random number generator
Rolling a dice isn’t much fun if you know which number you will get. We must add a random number generator, using the C runtime library function rand(), so the dice will show a different number for every roll.
To use rand(), the first step is to initialize it using some seed value. If we don’t initialize it with any value or initialize it with a fixed value, the sequence of generated numbers will be the same every time we run the app, which isn’t what we want to happen. For the purpose of this tutorial, we’ll use the current CPU time to seed the random number generator. Add the following code to the Game::Initialize() code:
void Game::Initialize() { Mesh::LoadFromFile(m_graphics, L"die.cmo", L"", L"", m_meshModels); srand ((unsigned int) time(NULL));
}
You will also need to include <time.h> at the beginning of Game.cpp for the time() function to be accessible:
#include "pch.h" #include "Game.h" #include <DirectXMath.h> #include <DirectXColors.h> #include <algorithm> #include <time.h>
After initializing, we can use the rand() function in our RollDie() method to calculate the roll. We will also need to set the target die rotations correctly for each of the rolls. To do that, replace the line that sets m_targetRotation so that the RollDie() method looks like this:
void Game::RollDie() { m_initialRotation = m_currentRotation;
int currentRoll = rand() % 6 + 1;
switch (currentRoll)
{
case 1:
m_targetRotation = XMFLOAT3(0.0f, 0.0f, 0.0f);
break;
case 2:
m_targetRotation = XMFLOAT3(0.0f, XM_PIDIV2, 0.0f);
break;
case 3:
m_targetRotation = XMFLOAT3(XM_PIDIV2, 0.0f, 0.0f);
break;
case 4:
m_targetRotation = XMFLOAT3(-1.0f * XM_PIDIV2, 0.0f, 0.0f);
break;
case 5:
m_targetRotation = XMFLOAT3(0.0f, -1.0f * XM_PIDIV2, 0.0f);
break;
case 6:
m_targetRotation = XMFLOAT3(0.0f, XM_PI, 0.0f);
break;
}
m_animationTime = 0.0f; m_isAnimationRunning = true; }
Now if you run the app, we have our animated die! You can roll the die by tapping anywhere on the screen. You can also check how it looks like on the snap view.
Make it jump!
This little app is already quite useful, but now we can make it much more interesting. This section will demonstrate how to add some flair by making the die jump when rolling, and adding some extra random spins to look more like a real die.
To add the “jump”, we will add another variable to our animation – the vertical (Y) coordinate. We will make this value change over time while the dice is rolling (in the Update() method), and we will change our Render() method to apply the translation to the cube. The first step is to add the translation variable to Game.h:
ref class Game sealed : public GameBase { // (snip) other class declarations...
private: std::vector<VSD3DStarter::Mesh*> m_meshModels; bool m_isAnimationRunning; float m_animationTime; DirectX::XMFLOAT3 m_initialRotation; DirectX::XMFLOAT3 m_currentRotation; DirectX::XMFLOAT3 m_targetRotation; float m_currentTranslationY; };
Then, make the value change over time on the Update() method:
void Game::Update(float timeTotal, float timeDelta) { if (m_isAnimationRunning) { // (snip) XMVECTOR current = initial + animationProgress * (target - initial); XMStoreFloat3(&m_currentRotation, current);
const float maxHeight = 2.0f;
m_currentTranslationY = 4.0f * maxHeight * animationProgress * (1 - animationProgress);
if (animationProgress >= 1.0f) m_isAnimationRunning = false; } }
This function, for those who remember their high school math classes, is the equation of a parabola with poles at 0 and 1 and vertex at (0.5, maxHeight). This will make our cube go up and down with a realistic effect. You can see a graph of this function at WolframAlpha .
The last step is to use the calculated translation to change the cube’s transform during the rendering phase. To do that, add the following code to the Render method:
void Game::Render() { // (snip) clear...
m_d3dContext->ClearDepthStencilView( /* (snip) */ );
XMMATRIX transform = XMMatrixRotationRollPitchYawFromVector(XMLoadFloat3(&m_currentRotation));
transform *= XMMatrixTranslation(0.0f, m_currentTranslationY, 0.0f);
for (UINT i = 0; i < m_meshModels.size(); i++)
{
m_meshModels[i]->Render(m_graphics, transform);
}
// (snip) MSAA...
}
Running the app now and clicking the screen will result in a nice animation with a jumping die. One last step to make it look even better is to add some random spins on each axis whenever the die is rolled. To do that we only need to change the RollDie() method to add some random spins to the target rotation:
void Game::RollDie() { // (snip) initialization, roll and switch(currentRoll)
XMVECTOR target = XMLoadFloat3(&m_targetRotation);
XMVECTOR current = XMLoadFloat3(&m_currentRotation);
// account for current rotation
target += XMVectorFloor(current / XM_2PI) * XM_2PI;
// add -1, 0 or 1 extra spins
XMVECTOR randomVector = XMLoadFloat3(&XMFLOAT3(rand() % 3 - 1.0f, rand() % 3 - 1.0f, rand() % 3 - 1.0f));
target += randomVector * XM_2PI;
XMStoreFloat3(&m_targetRotation, target);
m_animationTime = 0.0f; m_isAnimationRunning = true; }
This code performs two changes to the target rotation:
- Adds the total number of full spins thus far to the target rotation, making each roll relative to the previous roll rather than relative to the initial state of the die.
- Adds -1, 0 or 1 extra full spins to the target relative rotation. To do that we create a vector with three random values chosen between -1, 0 and 1, and we multiply that by 2*PI (a full spin in radians).
Also note that we use XMVECTORs once again for faster calculation and to be able to write only one formula instead of one for the x, y and z components separately.
So this completes our app functionality. It’s definitely a more useful and interesting version of the classic random number generator. You can download this version on CodePlex (direct download link on the tile below).
We only have a few more steps to finish in order to make this app run on Windows RT and Windows Phone as well! We’ll cover these steps in our third and last blog post. Stay tuned!


 Light
Light Dark
Dark
0 comments