Documentation for C++20 Ranges

Sy Brand

Tyler Whitney

C++20 introduced Ranges to the standard library: a new way of expressing composable transformations on collections of data. This feature adds a huge amount of expressive power and flexibility to C++. As with many concepts in C++, that power comes with new concepts to learn, and some complexity which can be difficult to navigate.

One way of taming that complexity is through complete, clear, comprehensive documentation.

Christopher Di Bella and Sy Brand (one of the co-authors of this post) presented their ideas for C++ documentation in the era of concepts in their CppCon 2021 talk. Tyler Whitney (the other co-author, and manager of our C++ documentation at Microsoft) has expanded these ideas and exhaustively documented the range adaptors available in the standard library for you.

To check it out, go to <ranges> on Microsoft Learn.

In this post, we’ll talk through some of the complexity of using and documenting Ranges, and outline the principles behind the documentation which Tyler has written.

But first, a quick introduction to Ranges for those of you who are not familiar with the feature.

What are Ranges?

At a high level, a range is something that you can iterate over. A range is represented by an iterator that marks the beginning of the range, and a sentinel that marks the end of the range. The sentinel may be the same type as the begin iterator, or it may be different, which lets Ranges support operations which simple iterator pairs can’t. The C++ Standard Library containers such as vector and list are ranges. A range abstracts iterators in a way that simplifies and amplifies your ability to use the Standard Template Library (STL).

STL algorithms usually take iterators that point to the portion of the collection that they should operate on. For example, you could sort a vector with std::sort(myVector.begin(), myVector.end());. However, carrying out an algorithm across a range is such a common operation, we’d rather not have to retrieve the begin and end iterators every time. With ranges, you can instead call std::ranges::sort(myVector);.

But perhaps the most important benefit of ranges is that you can compose STL algorithms that operate on ranges in a style that’s reminiscent of functional programming.

Traditional C++ algorithms don’t compose well. For example, if you wanted to build a vector of squares from the elements in another vector that are divisible by three, you could write something like:

std::vector<int> input = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
std::vector<int> intermediate, output;

std::copy_if(input.begin(), input.end(), std::back_inserter(intermediate),
             [](const int i) { return i%3 == 0; });

std::transform(intermediate.begin(), intermediate.end(), std::back_inserter(output), [](const int i) {return i*i; });

With ranges, you can produce a range with the same values without the intermediate vector:

// requires /std:c++20
std::vector<int> input = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10};

auto output = input
    | std::views::filter([](const int n) {return n % 3 == 0; })
    | std::views::transform([](const int n) {return n * n; });

Besides being easier to read, this code avoids the memory allocation that’s required for the intermediate vector and its contents. It also allows you to compose two operations.

In the preceding code, each element that’s divisible by three is combined with an operation to square that element. The pipe (|) symbol chains the operations together and is read left to right.

Importantly, the range adaptors returned by std::views::filter and std::views::transform compute their results on-demand: i.e. those closures are only ever called when you ask for an item. This lets you express concepts like infinite ranges with ease.

However, not all ranges were created equal. Different ranges have different characteristics and capabilities, and it can be difficult to understand what operations you are able to carry out just by looking at function signatures and concept definitions. Let’s look at some of these differences.

Types of ranges

We used the example of sort() earlier. There are all sorts kinds of sorting algorithms with different performance characteristics. If we have a large enough range and want to sort in-place, then we’ll often reach for quicksort. However, this requires us to be able to swap any two arbitrary elements of the range.

It’s easy to see how we can do this for a std::vector, where we can index to any location in constant-time. But for something like std::forward_list, which is a singly-linked list, it suddenly seems prohibitively expensive.

As such, std::ranges::sort requires that the range you give it be a random-access range: one where you can access any element in constant-time like you can with std::vector. There’s a bunch of concepts in the standard library which can be used to check the access capabilities of a given range: whether it’s random-access, contiguous in memory, allows bidirectional iteration, allows only forward iteration, or is single-pass. These are all in the std::ranges namespace, and have names like random_access_range and bidirectional_range.

However, it’s not just the access capabilities we might need to know. For example, some algorithms have optimized implementations for when you can retrieve the size of your range in amortized constant-time (std::ranges::sized_range). Some ranges cannot be iterated over if they are const, or allow you to keep using iterators they give you even after the range itself has been destroyed.

Unfortunately, working out whether a given range will work with a given adaptor or algorithm can be difficult just looking at the function signatures and constraints. For example, to work out if a given range adaptor is const iterable, we need to check the signatures of begin and end, look for any const-qualified overloads, then check the constraints of those overloads to see if calling them would be valid for our use case.

Additionally, these characteristics can affect not only whether some code should compile, but also its performance. Due to the importance of these characteristics and the difficulty of extracting them from APIs, we as documenters should identify the set which users of ranges need to know and surface them in a clear way.

What users of ranges need to know

If you want to use a given range adapter, like std::views::transform, there are many different considerations.

Most importantly is: what does this range do? For something like filter, this is fairly clear. But for others like common, it’s not so obvious if you don’t have the necessary background knowledge. Naming is hard.

We also need to know the usual things such as: how do we construct this adaptor, what parameters does it take, what are its members? And of course, are there any usage examples we can leverage?

However, with Ranges there’s also all of the characteristics we mentioned in the last section, like whether or not the range is random-access. We’ve identified the following characteristics as the most important. These are taken from the top-level Learn article on view classes:

• Range adaptor: The range adaptor that creates the given view (e.g. std::views::transform for std::ranges::transform_view). You typically use a range adaptor to create a view rather than create a view class directly, so it should be listed for convenience.
• Underlying range: Views have different iterator requirements for the kind of underlying range that they can use, e.g. split_view requires that the underlying range is a forward_range.
• View iterator category: The iterator category of the view. When a view adapts a range, the iterator type for the view is typically the same as the iterator type of the underlying range. However, it might be different for some views.
• Element type: The type of the elements that the view’s iterator returns. For example, filter_view’s elements will be of the same type as the underlying range, but transform_view’s elements will be of the type which the transformation function returns.
• Sized: Whether the view can return the number of elements that it refers to in amortized constant time. Not all views can, e.g. filter_view.
• Common range: Whether the view is a common_range, which means that the begin iterator and sentinel types are the same. Common ranges are useful for older code that works with iterator pairs. An example is iterator pair constructors for a sequence container, like vector(ranges::begin(x), ranges::end(x)).
• Borrowed range: Whether the view is a borrowed range. borrowed_range<T> means you can use iterators for T after T is destroyed.
  • No standard container is a borrowed range because destroying the container destroys the elements and invalidates any iterators. In that case, we say that the iterators are left “dangling” after destruction.
• Is const iterable: Whether you can iterate over a const instance of the view. Not all const views can be iterated. If a view isn’t const iterable, you can’t iterate with for (const auto& element : as_const(theView)) or pass it to a function that takes a const reference to the view and then tries to iterate over it.

Our documentation

Tyler has exhaustively documented all of the range adaptors in the C++20 standard library following the above principles.

If you want to use a range adaptor, your first port of call should be our “Range adaptors” page, which gives high-level information about each range adaptor, alongside examples and links to the view classes which are created by those adaptation functions.

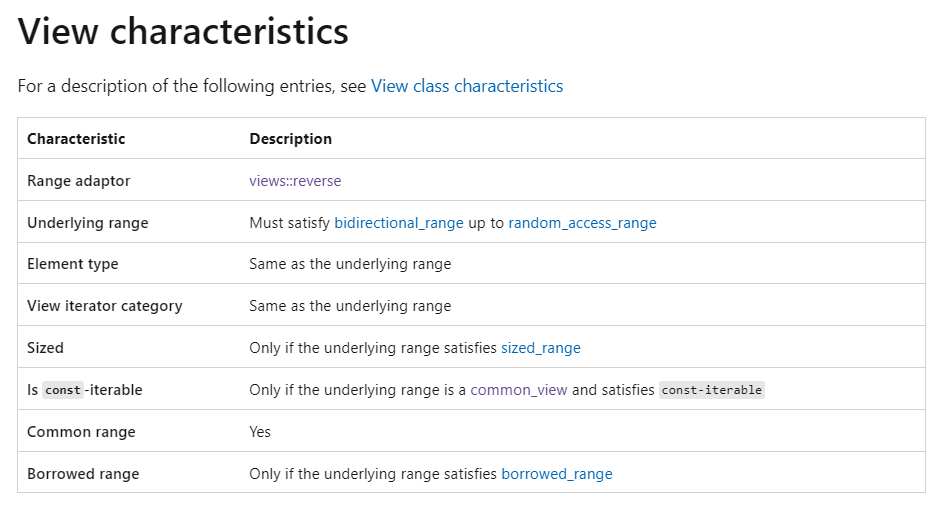
If you then need to know information about a given view class, such as whether it’s const iterable, or sized, you can then follow the link to the specific page for that type. For example, here’s the range characteristics for std::ranges::reverse_view, all neatly laid out:

We also have documentation for the concepts, functions, and alias templates defined in the <ranges> header.

Future Work

Currently all the range adaptors in the C++20 standard library have been documented. Several new ones have been added in C++23, but are not yet present in our docs.

Similarly, we are still working on documenting the huge amount of “rangified” algorithms which have been added to the standard library: the versions of functions in the <algorithm> header which now take ranges, are decorated with template constraints, and allow passing projection functions.

Send us your feedback

Please check out our Ranges documentation on Microsoft Learn and let us know your feedback! You can do so directly using the “Feedback” button near the top of the articles, or you can create a GitHub Issue using the buttons at the bottom of each page.

Sy Brand C++ Developer Advocate, C++ Team

Follow

Tyler Whitney

Follow