Towards Quantum at Scale

This spring we had the opportunity to mentor two student teams as part of the University of Washington’s NSF Research Traineeship program Accelerating Quantum-Enabled Technologies (AQET). This year-long certificate program offers graduate students training in quantum information science and engineering and includes several courses on different areas of quantum technologies followed by the culminating team project within the UW EE522: Quantum Information Practicum class. For this course the students worked on a quantum-related project under the guidance of mentors from the quantum industry—and that’s where we came in.

We worked on two projects focused on the tools necessary to implement quantum algorithms at scale. As quantum computers evolve from their current noisy intermediate scale quantum (NISQ) era to scalable quantum supercomputers, the programs that run on them will evolve as well, from simple circuits to complex programs that solve sophisticated problems. As part of this progress, we start exploring the practicality of implementing various algorithms to run on quantum computers and the resources required to execute them. We also look at the possibility of generating parts of these programs automatically, borrowing from our experience in classical computing. The students’ projects explored different areas of quantum software development using Microsoft’s Quantum Development Kit (QDK) and Azure Quantum Resource Estimator.

Both teams did a great job, and later this fall they will be presenting their work at IEEE Quantum Week 2023 on Wednesday, September 20. Here is a teaser of their work.

Project 1: Integrating Automatic Quantum Oracle Synthesis into Quantum Development Kit for Resource Estimation

Students: Chaman Gupta, I-Tung Chen

Mentors: Mathias Soeken, Mariia Mykhailova

The goal of this project was to design a workflow that would convert classical computation description into Q# code that implements it as a quantum computation. For example, the following Q# code for classical computation

    internal function Multiplication2(a : Int, b : Int) : Int {

        return a * b;

    }

would be automatically converted into a quantum circuit that can be used like an operation implemented by the Q# library operation, e.g., MultiplyI.

The QDK samples already had an example of doing this for Boolean function evaluation, so this project targeted integers and arithmetic functions that work with integers: addition, multiplication, and modulo operations.

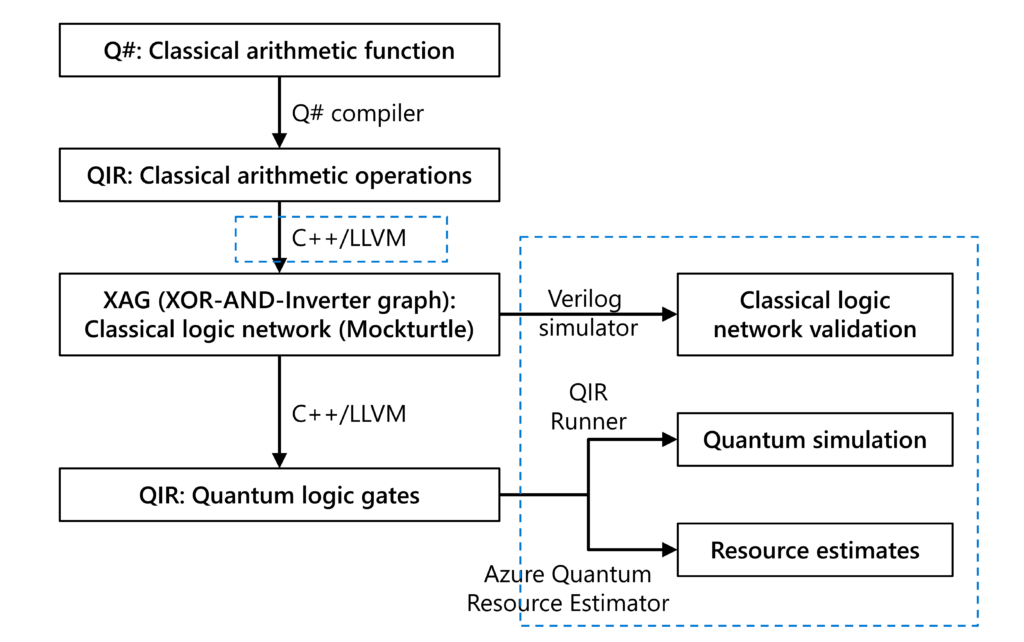
The image below shows the workflow used in the project.

Automated oracle synthesis workflow as implemented in the project

The steps in the workflow are as follows.

• The classical computation that needs to be converted into quantum is defined as a Q# function using the Int data type and built-in arithmetic for it, as shown in the above code snippet.
• The Q# compiler converts this function definition into equivalent Quantum Intermediate Representation (QIR) code.
• The automatic synthesis program reads the QIR code and converts it into an XAG (XOR-AND-Inverter graph) representation.
• This representation is optimized using the Mockturtle library—a C++ library for logic network manipulations. Up to this point, all the code represented remained classical.
• Finally, the automatic synthesis program converts the optimized XAG representation into a corresponding sequence of quantum logic gates in QIR that implements the original classical computation.

The generated quantum code can be executed via any tool that accepts QIR programs as input. This project used QIR Runner to run the simulation of the generated code for small inputs, and Azure Quantum Resource Estimator to estimate the resources required to run the code for larger inputs. Code samples and more technical details of this work can be found here.

Results and next steps

When compared with handcrafted Q# library operations implementing similar quantum computations, our automatically generated code was faster but required more qubits to run. This shows that automatic generation of quantum code is a promising avenue of producing reliable and performant code in an efficient manner. The next steps in this direction would be exploring the ways to optimize the generated code even further and adding support for more arithmetic types and operations, such as floating-point arithmetic.

Project 2: Quantum Resource Estimation of Arithmetic Primitives

Students: Ethan Hansen, Sanskriti Joshi, Hannah Rarick

Mentors: Wim van Dam, Mariia Mykhailova

In this project, the students explored quantum multiplication algorithms and compared their efficiency in terms of runtime, qubit numbers, and T-gates required to run them on large inputs.

The project built on prior work by Gidney and it compared three quantum implementations of algorithms for multiplying n-bit integers:

1. “Schoolbook” multiplication is the standard approach of multiplying the multiplicand by each bit of the multiplier and then adding together the results with proper shifts in positions. For n-bit integers this algorithm has complexity proportional to n².
2. Karatsuba multiplication splits the inputs u and v into halves u= a + 2^hb and v = x + 2^hy and computes their product u∙v = (a + 2^hb)(x + 2^hy) as a∙x + 2^2h(b∙y) + 2^h[(a + b)∙(x + y) − ax − by], thus reducing multiplication of two n-bit integers to three multiplications of two (n/2)-bit integers. The time asymptotic complexity of this algorithm is proportional to n^1.58.
3. Windowed multiplication is applicable when a quantum integer is to be multiplied by a classical constant and utilizes classically precomputed lookup tables to merge parts of operations.

Classical multiplication is an arithmetic operation that is often taken for granted when discussing algorithms. However, when implemented on a quantum computer, it incurs quite a lot of overhead in terms of both additional qubits and extra operations performed to implement the computation as a unitary transformation that preserves coherence.

Results and next steps

Using Azure Quantum Resource Estimator, the team calculated how the required resources depend on the multiplication algorithm used and on the size of the integers. The estimates showed that windowed multiplication uses slightly more qubits compared to the schoolbook algorithm but that it runs faster. Karatsuba’s algorithm uses more qubits and has longer runtimes compared to the schoolbook algorithm for inputs up to several thousand bits long. Eventually though, for large enough input sizes, the runtime of Karatsuba’s algorithm caught up with that of the schoolbook algorithm. Put together, these results refine our understanding of the performance of these three algorithms, and how in different settings different algorithms should be preferred.

This project provides a framework of applying similar resource estimation techniques to comparing different implementations of other quantum arithmetic primitives, such as floating-point functions, and other quantum subroutines.

The students found their projects interesting and enjoyable. They mentioned that the work on capstone projects helped them discover and learn important topics in quantum computing, such as oracle synthesis and resource estimation of algorithms, and broaden their understanding of the current state of the field. The students got valuable insights into their projects using Azure Quantum Resource Estimator, and their feedback on their experience helped us improve the tool for the future users. It has been a pleasure to mentor these teams, and we are looking forward to next year’s capstone projects!

Want to know more?

• Are you planning to attend IEEE Quantum Week? Then check out the presentations of these projects at the 3rd International Workshop on Quantum Software Engineering and Technology on Wednesday, September 20^th and learn more about resource estimation for quantum algorithms at the Quantum Resource Estimation workshop on Thursday, September 21^st.
• Check out the existing code sample for automatic oracle generation and the students’ work that adds support for integers and integer operations.
• Learn more about quantum resource estimation, Azure Quantum’s Resource Estimator, and the technical background behind this tool.