Azure Quantum Integrated Hybrid unlocks algorithmic primitives
To build a quantum supercomputer that can solve the world’s hardest and most complex problems in chemistry and materials science, several key ingredients need to come together. First, today’s foundational-level quantum machines need to be scaled up to a size of at least one million stable and controllable qubits. These are the table stakes for solving any interesting, useful algorithmic problem better or faster than a classical computer, based on what we know from profiling quantum programs using the Azure Quantum resource estimator.
Second, they need to be kept stable which means that error correction will be needed to combat the fundamental noise processes that disrupt the quantum computer. To create such stability basically means to forge the underlying noisy physical qubits into more stable logical qubits and to use fault-tolerant methods to implement operations. Microsoft’s unique topological qubit design has stability built in at the hardware level, and in turn will require less overhead to realize logical, fault-tolerant computation with a quantum error correcting code. No matter the underlying qubit design, advanced classical computational power will be required to keep a quantum machine stable, along with the underlying quantum error correcting code.
Finally, a quantum supercomputer will necessarily be hybrid, both in its implementation but also in the solutions it runs. After all, all quantum algorithms require a combination of both quantum and classical compute to produce a solution. And it is in this careful design of the classical and quantum compute, together, where we will see future innovation and new types of solutions emerging. Hybrid quantum computing enables the seamless integration of quantum and classical compute together. This is an important part for achieving our path to quantum at scale and to integrate our quantum machine alongside supercomputing classical machines in the cloud.
Implementing hybrid quantum algorithms
Integrated Hybrid in Azure Quantum allows to mix classical and quantum code together already today. “This opens the door to a new generation of hybrid algorithms that can benefit from complex side-computations that happen while the quantum state of the processor stays coherent”, Natalie Brown, Senior Advanced Physicist at Quantinuum.
- Magic State Distillation (MSD) protocols are quantum error-correction methods to create special quantum states that have preferrable properties for implementing universal, programmable quantum computers. Like in classical distillation which is the process of separating components of a liquid mixture by boiling and condensation, in quantum distillation the idea is to separate the noisy part of a quantum state and retain the good part. The hybrid nature of the quantum protocol manifests itself in a repeat loop that keeps running until a certain measurement result is seen. Afterward, the system is found in the distilled state, and the computation continues with the resource state.
A visualization of the protocol is shown here: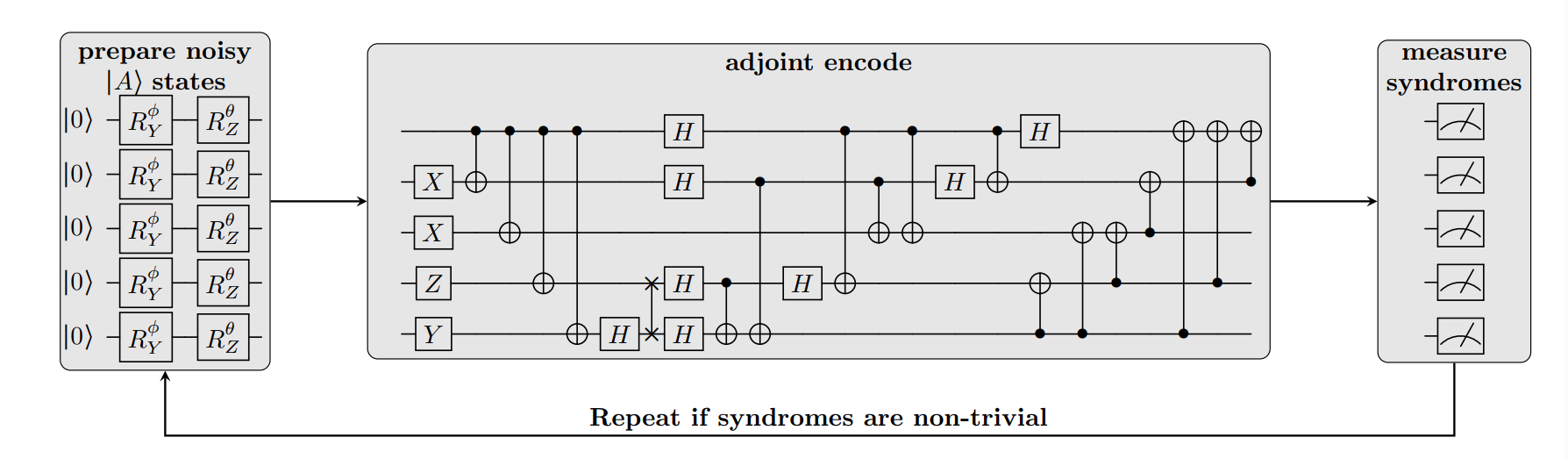 
The number of repetitions of the loop of the middle block depends on the measurement outcome and cannot be determined in advance, i.e., this program cannot be implemented as a static quantum circuit. Once the measurements of the 4 lower qubits indicate the result “0000”, the top most qubit is passed on as the output of the computation. In case any other syndrome is measured, the 5 qubits are reset and the procedure starts over.
- Repeat-Until-Success (RUS) protocols are algorithmic primitives that allow to implement complex quantum instructions that are not found in the basic instruction set with high accuracy. RUS protocols allow to implement a complex target operation that in a way can be best described as “speculative”: a simple operation is applied to a system that is larger than the original system on which the input state lives. Part of this large system is measured, and the quantum state is partially collapsed. If the measurement yields the correct result, the target operation is implemented perfectly. If the result is wrong, the input state does not undergo any damage, allowing the procedure to be tried again.Shown below is a visualization of a particular RUS protocol that implements a two-stage RUS circuit with two ancilla qubits to implement the unitary V3 = (I + 2iZ)/ √ 5 , which is a rotation around an irrational angle.
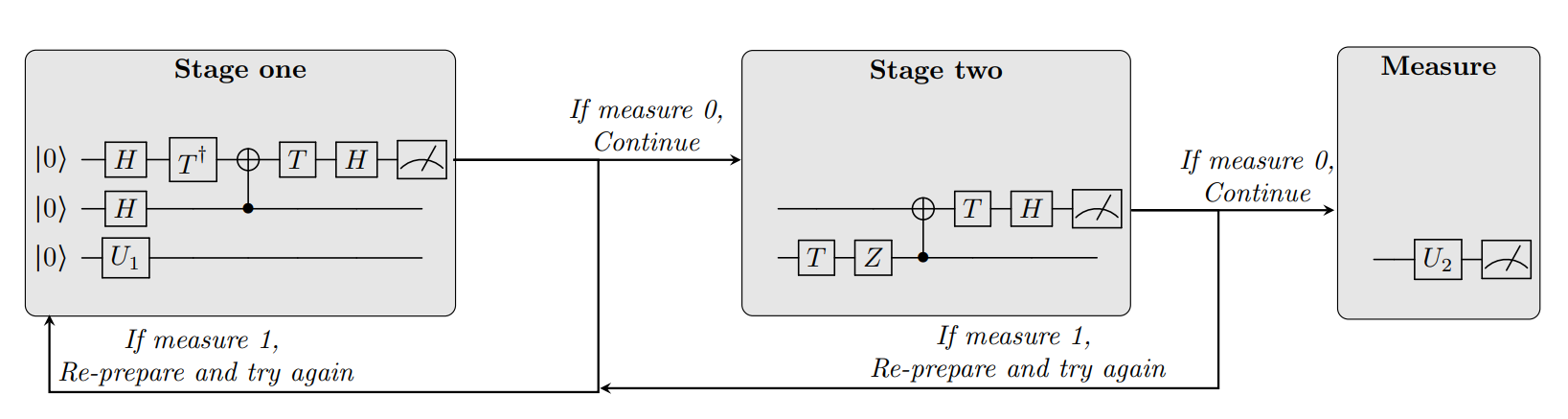Similar to MSD, RUS circuits require real-time feedback and control, as the success of the circuit depends on the measurement outcomes. Moreover, RUS circuits allow trade-offs between circuit representations, such as using recursion or loops, which may affect the performance and scalability of the circuit. To explore these trade-offs, we need a flexible representation that can express different versions of RUS circuits and compare their results.
What these two quantum algorithms both have in common is that they require complex control flow, including measurements that are applied during the computation while some part of the quantum computer remains coherent.
Experimental results
Recently, as shared in a paper posted on arxiv.org, a team of researchers from Microsoft and Quantinuum developed and ran MSD and RUS algorithms on the H1-Series in Azure Quantum.
The programs for the applications were written in Q# and were then compiled to the Quantum Intermediate Representation (QIR), which is based on LLVM, a representation widely used in classical compilers. QIR allows to represent quantum and classical logic using function declarations, basic blocks, and control flow instructions. QIR also enables us to use existing LLVM tools and techniques to analyze and optimize the program logic (eliminating unnecessary instructions and reducing transport steps), such as constant folding, loop unrolling, and dead code elimination.
Quantinuum’s H1-Series quantum computer leverages QIR in a powerful way: the Quantinuum quantum computer allows for hybrid classical/quantum programs to be executed. On the classical side, rich control flow is supported through integration with QIR including:
- Nested conditional statements,
- Mid-circuit measurements and branching depending on results,
- Re-use of already measured qubits,
- Classical function calls.
These primitive building blocks can be used to orchestrate computations such as MSD and RUS.
MSD protocol based on the [[5,1,3]] quantum error-correcting code
The left side of the following figure shows the expectation values for the actual run on Quantinuum H1-1 system, as well as the results of a simulation run of the H1-1 emulator (denoted as H1-1E). We plot the expectations with respect to three different Pauli frames X, Y, and Z which completely characterize the state of the qubits. The boxes indicate the ideal result which is only achievable for gates that are completely noiseless. The right side of the figure shows the probability of distillation succeeding at different limits, running both on the H1-1 system and the H1-1E emulator. The dashed black line indicates the probability of success expected for a perfect state preparation on a noiseless device.
 |
 |
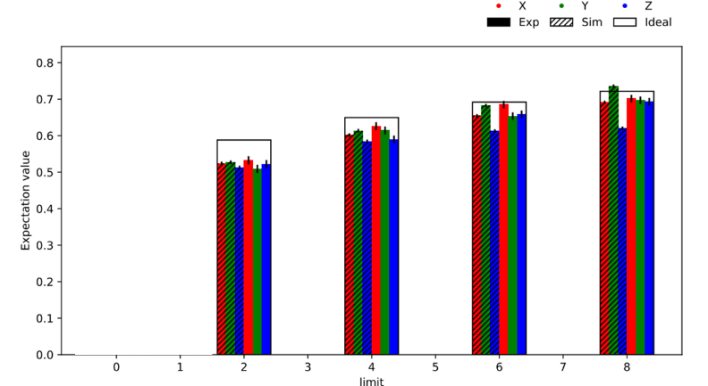Two-stage RUS circuit
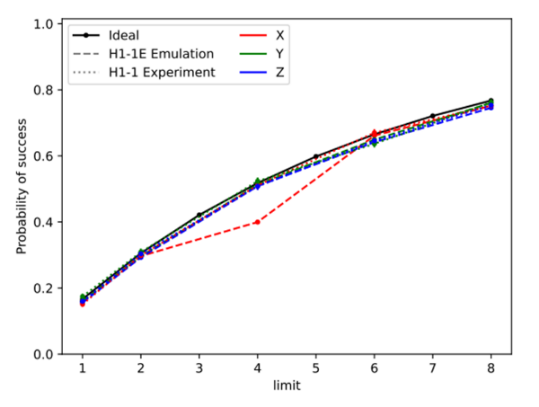
Researchers demonstrated the viability of this RUS protocol using QIR on Quantinuum’s QCCD simulator, which models realistic noise and errors in trapped ion systems, and by running it on the actual device. QIR was used to express four different versions of the RUS circuit, each using a different combination of recursion or loops, and Q# or OpenQASM as the source language.
 |
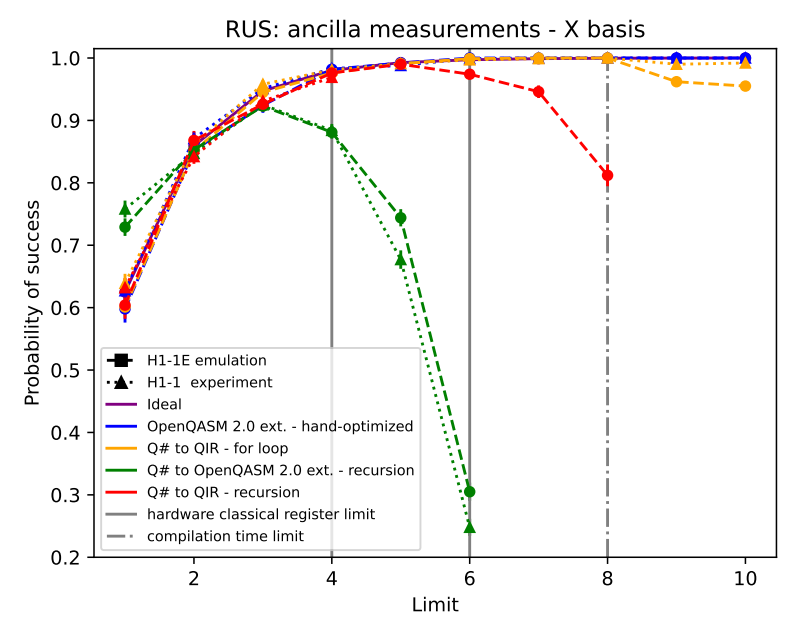As shown in the figure on the left above, the RUS protocol shows best performance when the Q# to QIR compiler is used and applied to a Q# implementation that realizes the RUS protocol as a for loop. As the iteration limit is increased, there is a clear drop in the performance for the recursion implementations, while the performance of loop implementations closely tracks the hand optimized OpenQASM 2.0++ code which is only achievable for gates that are completely noiseless.
A full Q# code sample that runs in Azure Quantum and that implements this hybrid program can be found at https://aka.ms/AQ/Samples/RUS.
Conclusion
In this blog post, we have shown how Q# can be used to implement and optimize fault-tolerant protocols that use a hybrid approach of quantum and classical logic. We have presented two examples of such protocols, MSD and RUS circuits, and demonstrated their execution and performance through Azure Quantum on Quantinuum’s H1 series system that runs on an ion trap quantum charge-coupled device architecture platform. We have also shown how QIR can leverage the LLVM toolchain to enable interoperability and portability across different quantum hardware platforms.
Learn more and get started with Azure Quantum today
- Whether you’re starting your own learning journey, exploring quantum hardware, or developing quantum algorithms for the future, Azure Quantum offers a platform for your quantum exploration and innovation.
- For enterprises interested in accelerating scientific discovery today, you can learn more about the recently announced Azure Quantum Elements, Microsoft’s system for computational chemistry and materials science combining the latest breakthroughs in HPC, AI, and quantum computing.
- At Microsoft, we are architecting a public cloud with Azure that enables scaled quantum computing to become a reality and then seamlessly delivers the profound benefits of it to our customers. Learn more about how Microsoft is harnessing the power of the cloud to make the promise of quantum at scale a reality and join our Microsoft Quantum Innovator Series with distinguished speakers that provide unique insights into Microsoft’s quantum computing effort.
#quantumcomputing #quantumcloud #azurequantum #quantinuum #QIR
Light
Dark
0 comments