Hi, my name is Eric Brumer. I’m a developer on the C++ compiler optimizer, but I’ve spent some time working on Project Code Name Austin to help showcase the power and performance of C++ in a real world program. For a general overview of the project, please check out the introduction blog post.
This blog post describes how we perform ink smoothing.
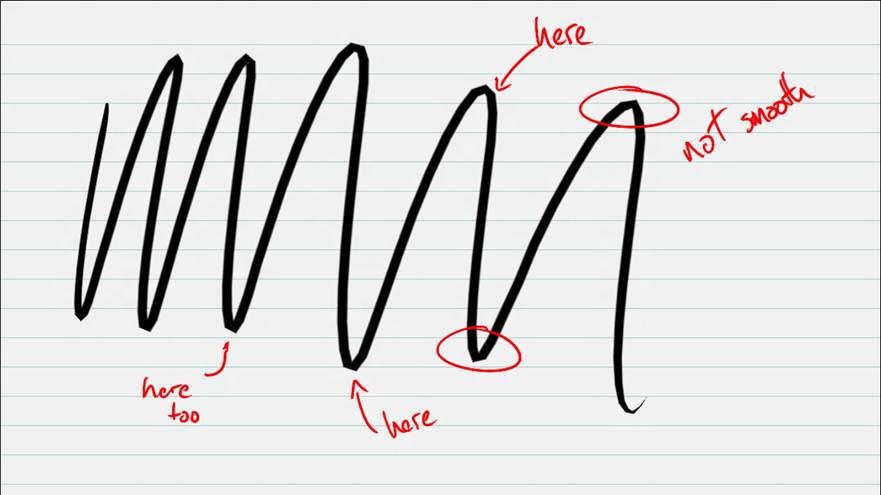
Consider a straightforward ink drawing mechanism: draw straight lines between each stylus input point that is sampled. The devices and drivers we have been using on Windows 8 sample 120 input points per second. This may seem like a lot, but very swift strokes can sometimes cause visible straight edges. Here’s a sample from the app (without ink smoothing) which shows some straight edges:
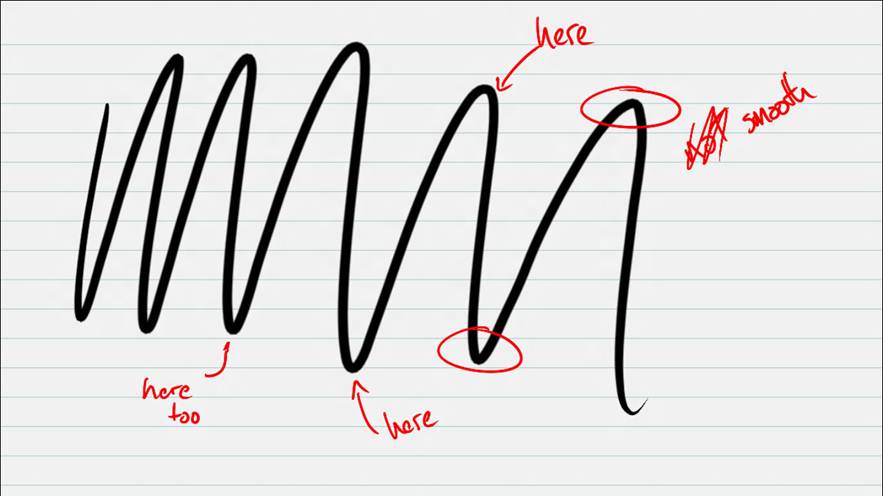
Here is the same set of ink strokes, but with the ink stroke smoothed.
Spline
We are using a spline technique to do real time ink smoothing. Other options were considered, but the spline (a) can be done in real time so the strokes you draw are always smooth as new input points are sampled and (b) are computationally feasible.
There is plenty of literature online about spline smoothing techniques, but in my (limited) research I have either found descriptions that are too simplistic, or descriptions that require a degree in computer graphics to understand. So here’s my shot at something in the middle…
Before computers, a technique was used to create smoothed curves using a tool called a spline. This was a flexible material (heavy rope, a flexible piece of wood, etc) that could bend into shape, but also be fixed at certain locations along its body. For example, you could take a piece of heavy rope, pin the rope to a wall using a bunch of pins in different locations along the rope, then trace the outline of the bendy rope to yield a spline-smoothed curve.
Fast forward several decades and now we are using the same principles to create a smoothed line between a set of points. Say we have a line with many points P0, P1, P2, … To smooth it using a spline, we take the first 4 points (P0, P1, P2, P3) and draw a smooth curve that passes through P1 & P2. Then we move the window of 4 points to (P1, P2, P3, P4) and draw a smooth curve that passes through P2 & P3. Rinse and repeat for the entire curve. The reason it’s a spline technique is that we consider the two points as being ‘pinned’, just like pinning some rope to a wall.
Before going into how we draw the smoothed line between those points, let’s examine the benefits:
- We only need four points to draw a smoothed line between the middle two. As you are drawing an ink stroke with your stylus, we are constantly able to smooth the stroke. I.e. we can do real time smoothing.
- The computation is bounded, and by some neat compiler optimizations and limiting the number of samples when drawing the smoothed line (see item 2 below) we can ensure ink smoothing won’t be on the critical path of performance.
There are a few things to keep in mind:
- We need to handle drawing a smoothed line between the first two points (P0 & P1), as well as drawing the smoothed line between the last two points on the curve. I do these by faking up those points and applying the same spline technique.
- I keep writing “draw a smoothed line between two points”. We can’t draw a smoothed line; we can only draw a bunch of straight lines that look smooth. So when I say “draw a smoothed line between two points” what I mean to say is “draw many straight lines that look smooth which connect two points”. We just sample points along the curved line at regular intervals which are known to look smooth at the pixel level.
Cubic Spline & Cardinal Spline
Now on to the mathematical meat… When a graphics person says that a line is smooth at a given point, what they are saying is that the line is contiguous at that point, the first derivative of the line is contiguous at that point, and the second derivative is contiguous at that point. Apologies if I’m bringing back horrible memories of high school or college calculus.
Here’s a visual of five points with the smoothed line already drawn in blue.
We can define each segment of the smoothed blue curve as being parameterized by a parameter “t” which goes from 0 to 1. So the blue line is the concatenation of 4 curves given by:
P01(t) where t ranges from 0 to 1 for the first segment (from P0 to P1)
P12(t) where t ranges from 0 to 1 for the second segment (from P1 to P2)
… etc …
Using the ` character to mean derivative, applying the definition of smooth at the endpoints of each of the segments yields a bunch of equations:
P01(t=1) = P12(t=0) P`01(t=1) = P`12(t=0) P“01(t=1) = P“12(t=0)
P12(t=1) = P23(t=0) P`12(t=1) = P`23(t=0) P“12(t=1) = P“23(t=0)
… etc …
Solving those equations exactly is trying. See spline interpolation. In general, if you are looking for a polynomial to satisfy an equation with second derivatives, you are shopping for a polynomial of degree 3, aka a cubic polynomial. Hence the ‘cubic’ in cubic spline.
The Wikipedia page shows a solution to fit the smoothness equations, but a lot of work has been done in this space to come up with a more computationally feasible solution that looks just as smooth. Basically, we lessen the second derivative equations and say P“01(t=1) ~= P“12(t=0), etc. This opens up many possibilities – look up any cubic spline and you’ll see many options.
After much experimenting, I found that the Cardinal spline works best for our ink strokes. The cardinal spline solution for the smoothed curve between 4 points P0, P1, P2, P3 is as follows:
The factor L is used to simulate the “tension in the heavy rope”, and can be tuned as you see fit. We chose a value around 0.5. If you are so inclined, you can also write out P23(t), take a bunch of derivatives and see this fits the smoothness equations. If you are a high school calculus teacher, please don’t make your students do this for homework.
The formula can be expressed in C++:
for (int i=0; i<numPoints; i++)
{
float t = (float)i/(float)(numPoints-1);
smoothedPoints_X[i] = (2*t*t*t – 3*t*t + 1) * p2x
+ (-2*t*t*t + 3*t*t) * p3x
+ (t*t*t – 2*t*t + t) * L*(p3x-p1x)
+ (t*t*t – t*t) * L*(p4x-p2x);
smoothedPoints_Y[i] = (2*t*t*t – 3*t*t + 1) * p2y
+ (-2*t*t*t + 3*t*t) * p3y
+ (t*t*t – 2*t*t + t) * L*(p3y-p1y)
+ (t*t*t – t*t) * L*(p4y-p2y);
}
numPoints (the number of points to sample on our smoothed line) is based on the minimum interval for what we thought looked good.
Performance
Like I mentioned before, we do real-time ink smoothing. That is to say an ink stroke is smoothed as it is drawn. We need to make sure that drawing a smooth line does not take too long otherwise we’ll notice a drop in frame rate where the ink stroke lags behind your stylus.
One of the benefits of writing this app in C++ is the opportunity for compiler optimizations to kick in. In this particular case, the cardinal spline equations are auto-vectorized by the Visual Studio 2012 C++ compiler. This yields a 30% performance boost when smoothing ink strokes, ensuring we can smooth ink points as fast as Windows can sample them. Also, any extra computing time saved lets us (a) do more computations to make the app better, or (b) finish our computations early, putting the app to sleep thus saving power.
Read all about the auto vectorizer here: http://blogs.msdn.com/b/nativeconcurrency/archive/2012/04/12/auto-vectorizer-in-visual-studio-11-overview.aspx


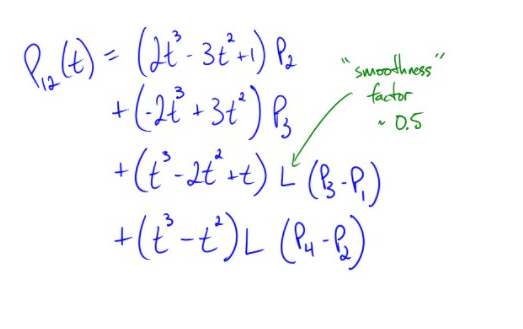
0 comments