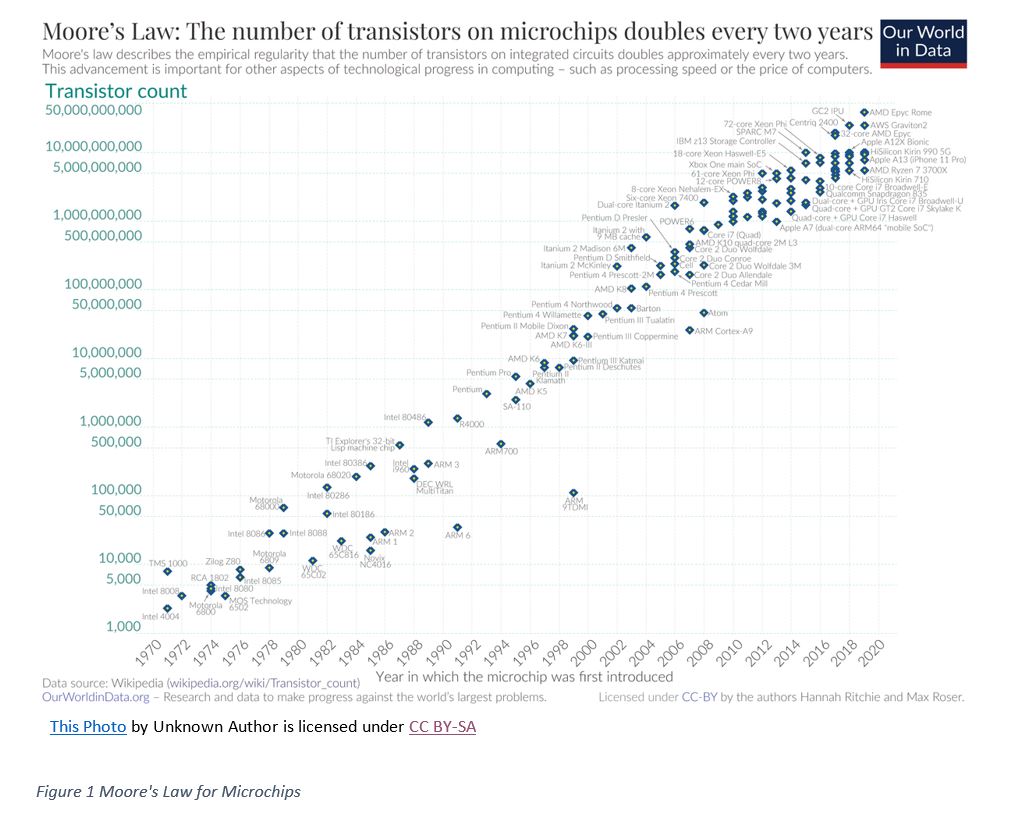
In 1975 Gordon Moore made a prediction which became famous as Moore’s law which states that the number of transistors in a microchip doubles every two years (or 18 months depending on who you talk to) (Figure 1). The simplified version of this law states that the processing power or processing speed doubles every two years. Translating to image sensors in general, does the number of pixels in a sensor double every two years or pixel size scale by √2 every two years. Not so fast, image sensors are more like analog chips than digital chips which do not scale proportionately with the technology node. RGB sensors have managed to scale the pixel size often to the detriment of performance because size/cost was of much greater importance. Process enhancements by targeted process improvements just in the pixel region or by stacking multiple wafers to move some of the processing to smaller geometry nodes have helped to a certain degree too.
Taking this into the realm of ToF Pixels, unlike the usual use of RGB image sensors, ToF pixel values need to be metrology grade because they support a measurement instead of needing the picture to look pretty. The performance is defined by signal-to-noise ratio. Let’s dig deeper into that. To simplify this analysis, there are three different regimes when looking at dominant noise sources.
- Signal Shot Noise
- Ambient Shot Noise
- Read Noise
Picking one regime for this blog post (e.g., Ambient Shot Noise) and going deeper into that (we can cover other regimes in other blog posts). If QE is the probability of collecting a photo charge from a photon and MC is the probability that a photo charge will generate a signal useful for acquiring depth, then:
Given we are at the upper limits of MC and QE, as pixel area is reduced by half, the temporal jitter increases by √2. Does that mean smaller pixels are doomed to poor performance? It turns out there is another lever to improve performance and that is modulation frequency. In Phase-based ToF methods as Cyrus wrote in his blog post . Stated differently, The temporal jitter can then be expressed as
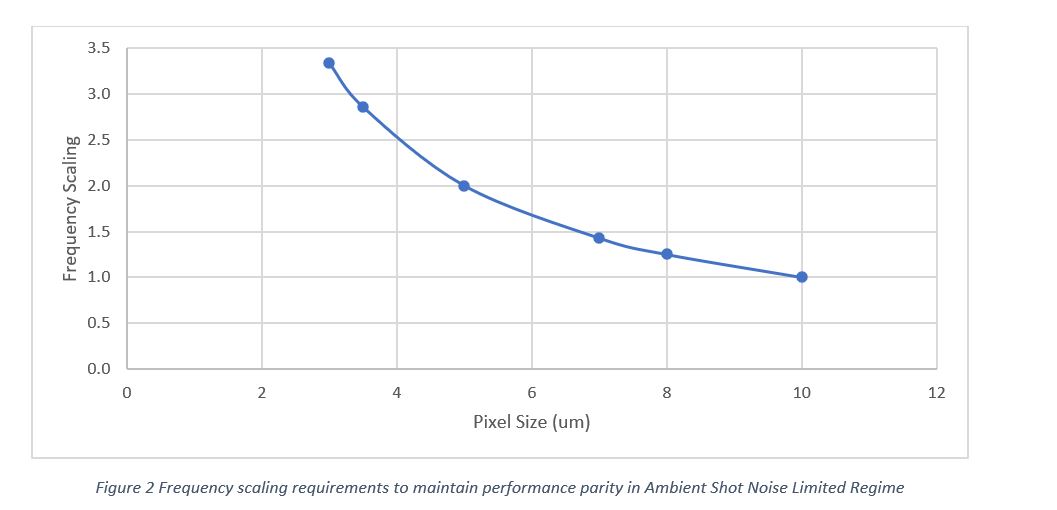
So, it would seem like you can recover the performance drop that occurs due to reducing pixel size by increasing the frequency (Figure 2). However, this is only possible if the modulation contrast (MC) doesn’t significantly degrade with higher frequencies. Microsoft ToF technology is a leader where MC at high frequencies is concerned (78% at 320 MHz). Also, higher frequency can increase both chip power and laser optical power. We can discuss ways to mitigate this in future blog posts. Stay tuned.
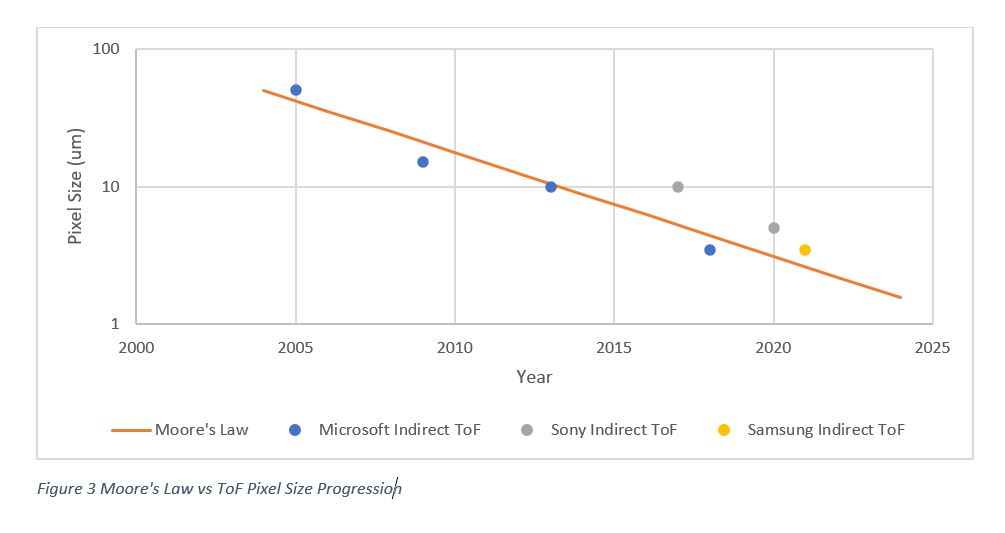
The following plot will speak for itself on whether we are on the right trajectory for ToF pixel scaling as pertains to Moore’s Law (Figure 3).


0 comments