Summary: Microsoft senior software engineer, Firaz Samet, shows how to use Windows PowerShell to approximate the value of pi from a polygon.

Microsoft Scripting Guy, Ed Wilson, is here. Today we have a guest blog post from Firaz Samet in honor of Pi (π) Day. I will turn the blog over…

The Scripting Guy ran across my PowerShell Math Module on CodePlex, and he asked me if I would be interested in writing a blog post for Pi Day. I was also incidentally thinking about Pi Day, so this came at the right time. I hope you enjoy reading it.

First a little bit about me…

I am a senior software engineer at Microsoft where I work on Azure Stream Analytics. I have been playing around with Windows PowerShell since version 1.0 where I worked on SharePoint search management cmdlets. I love the power it provides by accessing the full .NET Framework and its rich set of built-in cmdlets and filtering capabilities. I concede that its syntax needed some time to get used to, but after I went past that, it became a natural way to solve my most common scripting and programming needs. One thing that has always frustrated me is that mathematical notation is a bit cumbersome. One reason I wrote a wrapper around Math.NET is to help ease interactive matrix manipulation.

Pi Day is celebrated around the world on March 3 (3.14). It aims to raise interest in math and especially π. This year’s will be even more significant (3.1415…). For more information, see Pi Day on Wikipedia.

In this post, I will talk about using Windows PowerShell to approximate π with polygons. I will also introduce matrix calculus with Math.NET Numerics, using a thin Windows PowerShell wrapper called Math.NET PowerShell.

Approximating π

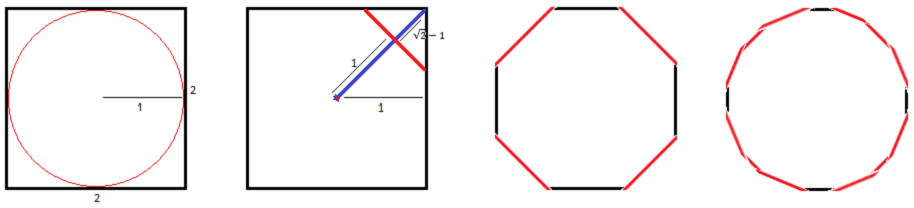
The approximation of π that I introduce here starts with a square with sides that measure 2 units. It then approximates the area of the inscribed unit circle (radius is 1 unit, of which the area equals π) by constructing a regular polygon with double the number of sides with each iteration. This is done by chopping off triangles from each corner area, while keeping the apothem to 1.

By using the triangle properties and the trigonometric half-angle formulae for the tangent, we can deduce the following formula:

Expressing the formula in Windows PowerShell

We now want to express the previous formula with Windows PowerShell. We will mainly use the [math] library’s power method, Pow(x, y). But to make the notation simpler, we will introduce a Windows PowerShell filter to make calling the Pow method closer to the mathematical notation:

filter ^([double] $y){[math]::Pow($_,$y)}

This means that expressing 2³ would look like (2 |^ 3) instead of [math]::Pow(2, 3). Parentheses are still required to prevent the pipeline syntax from affecting the remainder of the code. Similarly,  will become (2 |^ .5).

We now use Windows PowerShell to develop the formula:

function halfTan($t){$t / (((($t |^ 2) + 1) |^ .5) + 1)}

function triangleArea($t){2 * ($t |^ 3) / (-($t |^ 2) + 1)}

$t = 1

$t = halfTan $t

$a = ((2 |^ .5) – 1) |^ 2

$p = 4

0..25 | %{

     $i = $_;

     $p-= $a * 4 * (2 |^ $i);

     "{0} t: {1}  a: {2}  ~pi:{3}" -f $i,$t,$a,$p;

     $t = halfTan $t;

     $a = triangleArea $t;

}

On iteration 25, we reach the value of [math]::Pi.

24 t: 2.34066892682746E-08  a: 2.56477909373991E-23  ~pi:3.14159265358979

Matrix expression

The iterative nature ofmakes using matrices an interesting proposition. For this reason, we will express it in the following matrix formula:

We will then use a thin Windows PowerShell wrapper around Math.NET Numerics called Math.NET PowerShell to calculate it in Windows PowerShell. The Windows PowerShell module offers a familiar way to initialize matrices (such as m "1 0;0 1" to initialize the identity matrix of order 2) and an easy approach to using the adequate Math.NET Numerics matrix type.

By default, Math.NET PowerShell uses the most memory conservative matrix type (sparse matrix with single precision). But the precision of this type is too low for our needs. Therefore, we will select the double precision type. This is achieved by using the following command:

Set-MathNetMatrixType Double

When this is done, we express the formula using the previous matrix notation as follows:

function halfTan($t){$t / (((($t |^ 2) + 1) |^ .5) + 1)}

function triangleArea($t){2 * ($t |^ 3) / (-($t |^ 2) + 1)}

$t = 1

$t = halfTan $t;

$p = m "4 -4;0 0"

$area = m "1 0;0 2"

$area[1,0]=((2 |^ .5) – 1) |^ 2

$p=$p*$area

0..25 | %{

"{0} t: {1}  a: {2}  ~pi:{3}" -f $_,$t,$area[1,0],$p[0,0];

$t = halfTan $t;

$area[1,0] = triangleArea $t

$p=$p*$area

}

Running this script yields the same approximation for π.

~ Firaz

Thank you for writing a most interesting article, Firaz.

I invite you to follow me on Twitter and Facebook. If you have any questions, send email to me at scripter@microsoft.com, or post your questions on the Official Scripting Guys Forum. See you tomorrow. Until then, peace.

Ed Wilson, Microsoft Scripting Guy