
Microsoft Quantum Technical Blog
Q#
Focus blog
by Duis Aute, Principal Quantum Software Engineer
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris..

Q#
Microsoft's quantum programming language designed for developing and running quantum algorithms efficiently.
QIR
A standardized, hardware-agnostic intermediate representation for quantum programs.
Resource Estimation
Analyzes quantum algorithms to predict the required qubits, runtime, and other resources needed for execution on a quantum compute.
Partnerships and Announcements
Explore collaborative efforts driving innovation in the quantum ecosystem.
Browse all
No results found
Q#August 1, 2024
Resource Estimation Challenge at QRISE 2024: Recap
QIRJuly 29, 2024
Integrated Hybrid Support in the Azure Quantum Development Kit

Q#June 19, 2024
Evaluating cat qubits for fault-tolerant quantum computing using Resource Estimator

Q#May 20, 2024
Circuit Diagrams with Q#
Resource EstimationFebruary 28, 2024
Exploring space-time tradeoffs with Azure Quantum Resource Estimator
Resource EstimationJanuary 16, 2024
Design Fault Tolerant Quantum Computing applications with the Resource Estimator

Q#January 12, 2024
Announcing v1.0 of the Azure Quantum Development Kit
Q#November 29, 2023
Defining logical qubits: Criteria for Resilient Quantum Computation
Resource EstimationNovember 1, 2023
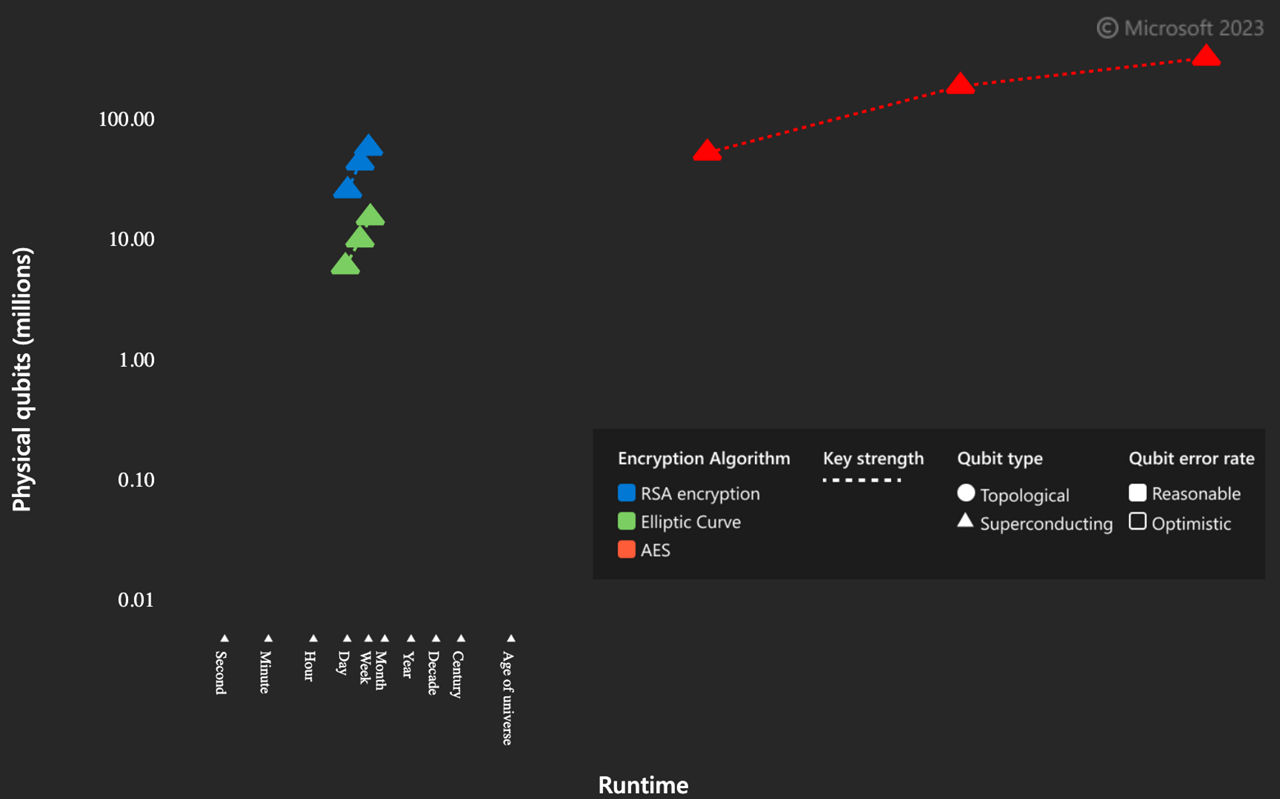
Calculating resource estimates for cryptanalysis
Join the email list
Join our email list for the latest updates and insights
— stay informed and ahead!




