Parallel Merge Sort using Barrier
Sorting is one of the most fundamental problems in software algorithms; there are many sequential sorting algorithms with different time and memory complexities, but when it comes to parallel sort, things get more complicated. I will explain a simple and scalable algorithm to write a parallel sort using the .NET 4.0 System.Threading.Barrier synchronization primitive.
Overview
MergeSort algorithm is a good candidate to parallelize, especially the first step where each thread can sort a separate partition independently then merging all these sorted partitions together to get the full array sorted.
Assuming the array length is N, it will be divided into M partitions P1, P2… Pm where M = number of threads. Thread0 will sort P0; Thread1 will sort P1 and so on. After this step, all threads need to be synchronized before starting the next phase, will do that using the Barrier synchronization primitive which will be initialized to total participant number of M. After all threads reach the barrier, every two continuous partitions will be merged together using one thread, so half of the threads will be eliminated after this phase, then we will have M/2 sorted partitions, so again every two new continuous partitions will be merged into a new one, and half of the threads will be eliminated, this step is repeated until the full array sorted.
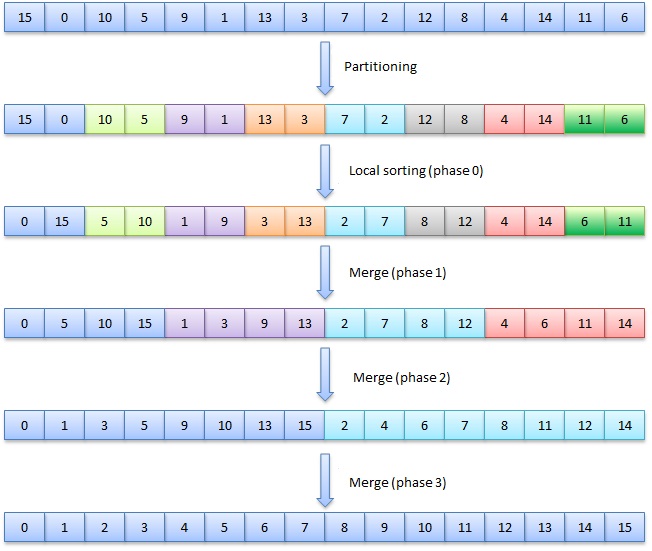
Algorithm Details
The new Parallel.Sort method is defined as:
public void Sort(T[] array, IComparer<T> comparer)
An auxiliary array is needed in each merge step of size Pi + Pi+1, to save these multiple allocations; the auxiliary array is allocated one time with the same input array size.
T[] auxArray = new T[array.Length];
Then the initial partition size and the number of workers are calculated, the number of merge iterations is determined by the number of workers, so for the sake of simplicity we will always assume that the number of workers is power of two.
int totalWorkers = Environment.ProcessorCount; // must be power of two // worker tasks, -1 because the main thread will be used as a worker too Task[] workers = new Task[totalWorkers - 1]; // number of iterations is determined by Log(workers), // this is why the workers has to be power of 2 int iterations = (int)Math.Log(totalWorkers, 2); // Number of elements for each array, if the elements // number is not divisible by the workers, the remainders // will be added to the first worker (the main thread) int partitionSize = array.Length / totalWorkers; int remainder = array.Length % totalWorkers;
Then the Barrier is initialized with total number of workers and a post phase action that does two things:
- Double the partition size after each iteration
- Swap the array and auxArray pointers (will be explained later)
Barrier barrier = new Barrier(totalWorkers, (b) => { partitionSize <<= 1; var temp = auxArray; auxArray = array; array = temp; });
Now we are ready for the actual logic by defining the work delegate that will be invoked by the workers, this delegate will does the following:
- Calculate the partition boundary using the partition index parameter
- Sort the partition using QuickSort algorithm (we can also use any other sort algorithm)
- Synchronize with all other workers using Barrier.SignalAndWait method to finish the first phase.
- Then will start the merge steps in Log(M) iterations, and in each iteration:
- Half of the workers are eliminated
- Merge the continuous partitions
- Update the new partition index and upper boundary
- Synchronize with the remaining workers using using Barrier.SignalAndWait method
Action<object> workAction = (obj) => { int index = (int)obj; //calculate the partition boundary int low = index * partitionSize; if (index > 0) low += remainder; int high = (index + 1) * partitionSize - 1 + remainder; QuickSort(array, low, high); barrier.SignalAndWait(); for (int j = 0; j < iterations; j++) { //we always remove the odd workers if (index % 2 == 1) { barrier.RemoveParticipant(); break; } int newHigh = high + partitionSize / 2; index >>= 1; //update the index after removing the zombie workers Merge(array, auxArray, low, high, high + 1, newHigh); high = newHigh; barrier.SignalAndWait(); } };
And finally we start the workers tasks with partitions indices; Partition 0 will be invoked by the main thread because it will be the only partition after the array is sorted.
for (int i = 0; i < workers.Length; i++) { workers[i] = Task.Factory.StartNew(obj => workAction(obj), i + 1); } workAction(0);
As you see in each merge iteration the Merge method is called to merge two partitions, this method takes the destination array in the first argument and the source array in the second argument and this is why we swap the two arrays in the post phase action, after each iteration we use one of the arrays as the source and the other one as the destination. But this mean if the number iterations is Odd (ex: on 8 cores machine you will get 3 iterations) this means the auxArray will have the full sorted array at the end, so in this case we need to do a full Array.Copy from the auxArray to the original array before we return from the method.
if (iterations % 2 != 0) Array.Copy(auxArray, array, array.Length);
Performance Benchmarks
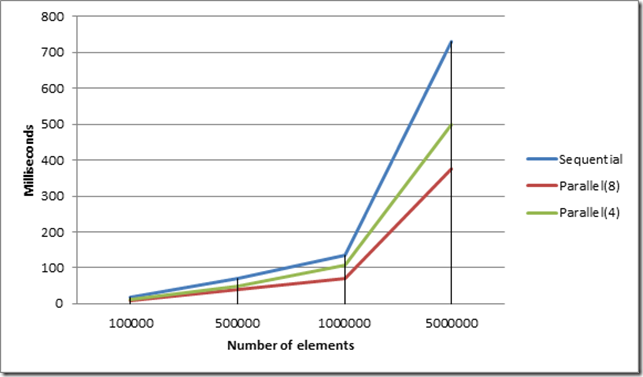
We measured the elapsed time of this algorithm versus the sequential Array.Sort method to sort N integer elements on a two Intel Xeon E5620 Quad CPUs machine. We used 100000, 500000, 1000000, 5000000 values for N, and tried two versions of the parallel algorithm one with 4 threads only and the other one with the complete 8 threads.
The graph shows that algorithm scales nicely for different number of threads and elements, when using 8 threads; the total time is less than half of sequential time for all values of N elements. Of course this algorithm can be improved more by parallelizing the merge step as well, but this will make the algorithm more complicated.

 Light
Light Dark
Dark
0 comments