Quantum Computing for Software Developers – Part I

Developer Support

App Dev Manager Leonard Woody breaks down the fundamentals of quantum computing from the perspective of a software developer.

The underpinnings of quantum computing (QC) is quantum mechanics. Unfortunately, quantum mechanics is very weird and hard to understand. Most articles on QC are of the pop science variety and introductions to QC are usually heavy on mathematics (linear algebra). I want to do something different. I want to explain QC using the language of software development.

So let’s get started! We are all familiar with the classical binary digit or bit.

The analog to this in QC is the quantum bit or qubit. An electron’s spin can be used to physically represent this.

Now, let’s code all this up (I’m using pseudo-code throughout the article).

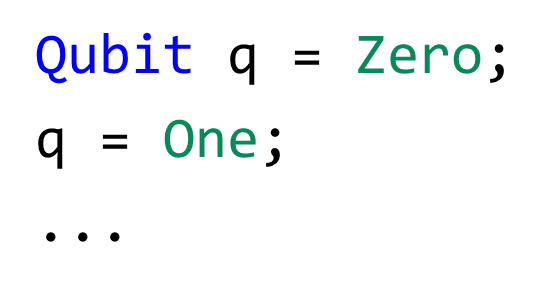
Superposition

The first major concept to understand in QC is superposition. I think it’s a horrible term in terms of describing what it actually is, but hey I’m not Richard Feynman. Superposition means that a qubit can be in the Zero state, the One state, or a combination of the Zero and One states.

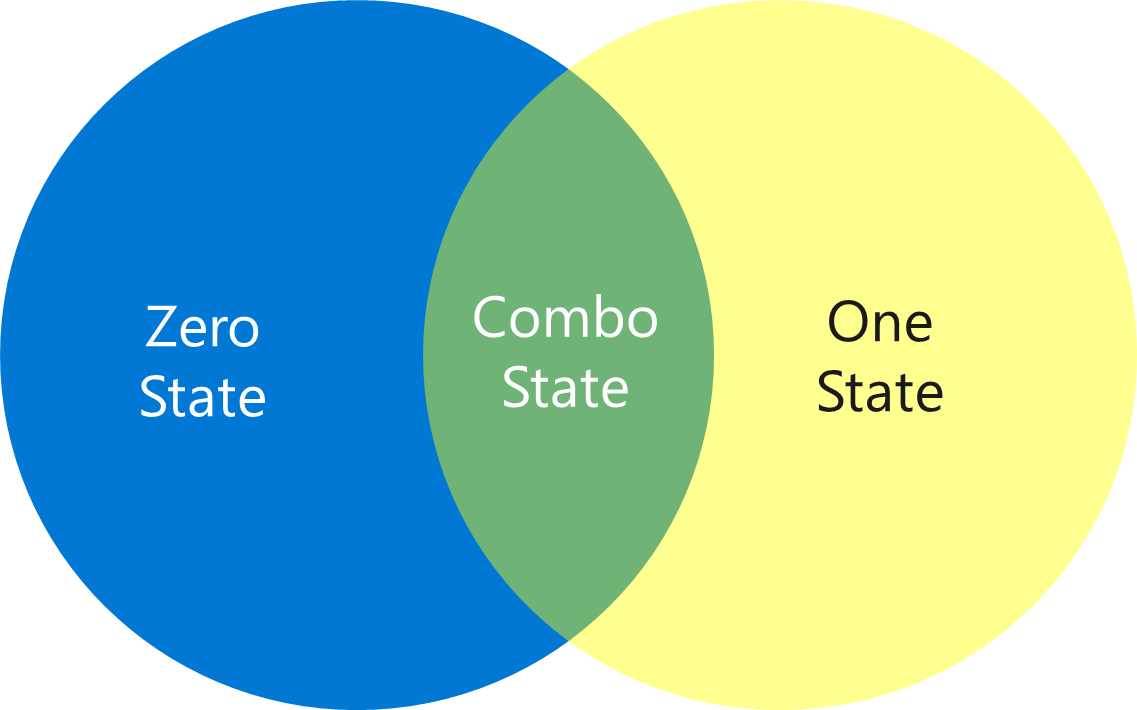
Think of it as a spinning coin, in which you can’t determine if it’s a 0 (tails) or 1 (heads).

https://youtu.be/PX64Ltc1uXU

Now, let’s do it in code!

Pretty weird, huh! In classical computing, the last statement would equal “b”. But in QC, it creates a whole new state or “number”.

Measurement

So the total possible states that a qubit can be in is infinite. But, when it is measured or “observed” it will always come out as 0 or 1. In code, it looks like this.

So now the question is, if the qubit is in some random state (a combination of the zero and one states), how do we know what the measurement will be? The code below shows the question better.

Well, the answer is another weird postulate of quantum mechanics. It is based on probability. Depending on the state the qubit is in, it could have a 50/50 chance of being a 0 or a 1. Or it could be 70/30. Whatever the probabilities are, they must add up to 100.

In part 2 of this blog series, I’ll go into how these probabilities are derived. Hope you enjoy the post!

Developer Support App Dev Customer Success Account Manager, Microsoft Developer Support

Follow