Math Accessibility Trees
This post discusses aspects of making mathematical equations accessible to blind people. Equations that are simple typographically, such as 𝐸 = 𝑚𝑐², are accessible with the use of standard left and right arrow key navigation and with each variable and two-dimensional construct being spoken or felt when the insertion point is moved to them. At an insertion point, the user can edit the equation using the regular keyboard input methods, perhaps based on UnicodeMath or LaTeX, or using a refreshable braille display using Nemeth Braille. But it can be hard to visualize a more typographically complex equation, let alone edit it. Instead, the user needs to be able to navigate a complex equation using a mathematical tree of the equation.
More than one kind of tree is possible and this post compares two trees for the equation
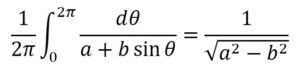
Each tree node is labeled with its math text in UnicodeMath along with the type of node. UnicodeMath lends itself to being spoken especially if processed a bit to speak things like 𝑎² as “a squared” in the current natural language as described in Speaking of math…. The first kind of tree corresponds to the traditional math layout used in documents, while the second kind corresponds to the mathematical semantics. Accordingly we call the first kind a display tree and the second a semantic tree.
More specifically, the display tree corresponds to the way TeX and OfficeMath display mathematical text and approximates the way Presentation MathML represents mathematical text. Mathematical layout entities such as fractions, integrals, roots, subscripts and superscripts are represented by nodes in trees. Binary and relational operators that don’t require special typography other than appropriate spacing are included in text nodes. The display tree for the equation above is
└─Math zone
└─ “1/2π ∫_0^2π ⅆ𝜃/(𝑎+𝑏 sin 𝜃) = 1/√(𝑎²−𝑏²)”
├─ “1/2π” fraction
│ ├─ “1” numerator
│ └─ “2π” denominator
├─ “∫_0^2π ⅆθ/(𝑎+𝑏 sin 𝜃)” integral
│ ├─ “0” lower limit
│ ├─ “2π” upper limit
│ └─ “ⅆθ/(𝑎+𝑏 sin 𝜃)” integrand
│ └─ “ⅆθ/(𝑎+𝑏 sin 𝜃)” fraction
│ ├─ “ⅆθ” numerator
│ └─ “𝑎+𝑏 sinθ” denominator
│ ├─ “𝑎+𝑏” text
│ └─ “sin𝜃” function apply
│ ├─ “sin” function name
│ └─ 𝜃” argument
├─ “=” text
└─ “1/√(𝑎²−𝑏²)” fraction
├─ “1” numerator
└─ “√(𝑎²−𝑏²)” denominator
└─ “√(𝑎²−𝑏²)” radical
├─ “⬚” degree
└─ “𝑎²−𝑏²” radicand
├─ “𝑎²” superscript
│ ├─ “𝑎” base
| └─ “2” script
├─ “−” text
└─ “𝑏²” superscript
├─ “𝑏” base
└─ “2” script
Note that the invisible times implicit between the leading fraction and the integral isn’t displayed and the expression 𝑎 + 𝑏 sinθ is displayed as a text node 𝑎 + 𝑏 followed by a function-apply node sinθ, without explicit nodes for the + and an implied invisible times.
To navigate through the 𝑎 + 𝑏 and into the fractions and integral, one can use the usual text left and right arrow keys or their braille equivalents. In OfficeMath, one can navigate through the whole equation with these arrow keys, but it’s helpful also to have coarser grained navigation keys to go between sibling nodes and up to parent nodes. For the sake of discussion, let’s suppose the tree navigation hot keys are those defined in the table
| Ctrl+→ | Go to next sibling |
| Ctrl+← | Go to previous sibling |
| Home | Go to parent ahead of current child |
| End | Go to parent after current child |
For example starting at the beginning of the equation, Ctrl+→ moves past the leading fraction to the integral, whereas → moves to the start of the numerator of the leading fraction. Starting at the beginning of the upper limit, Home goes to the insertion point between the leading fraction and the integral, while End goes to the insertion point in front of the equal sign. Ctrl+→ and Ctrl+← allow a user to scan an equation rapidly at any level in the hierarchy. After one of these hot keys is pressed, the linear format for the object at the new position can be spoken in a fashion quite similar to ClearSpeak. When the user finds a position of interest, s/he can use the usual input methods to delete and/or insert new math text.
Now consider the semantic tree, which allocates nodes to all binary and relational operators as well as to fractions, integrals, etc.
└─Math zone
└─ “1/2𝜋 ∫_0^2𝜋 ⅆ𝜃/(𝑎+𝑏 sin𝜃)=1/√(𝑎²− 𝑏²)”
└─ “=” text
├─ “⊠” implied times
│ ├─ “1/2𝜋” fraction
│ │ ├─ “1” numerator
│ │ └─ “2π” denominator
│ └─ “∫_0^2𝜋 ⅆ𝜃/(𝑎+𝑏 sin𝜃)” integral
│ ├─ “0” lower limit
│ ├─ “2π” upper limit
│ └─ “ⅆ𝜃/(𝑎+𝑏 sin𝜃)” integrand
│ └─ “ⅆ𝜃/(𝑎+𝑏 sin𝜃)” fraction
│ ├─ “ⅆ𝜃” numerator
│ │ └─ “⊠” implied times
│ │ ├─ “ⅆ” text
│ │ └─ “𝜃” text
│ └─ “𝑎+𝑏 sin𝜃” denominator
│ └─ “+” text
│ ├─ “𝑎” text
│ └─ “𝑏 sin𝜃” function apply
│ └─ “⊠” implied times
│ ├─ “𝑏” text
│ └─ “sin𝜃” function
│ └─ “” function apply
│ ├─ “sin” function name
│ └─ “𝜃” argument
└─ “1/√(𝑎²− 𝑏²)” fraction
├─ “1” numerator
└─ “√(𝑎²− 𝑏²)” denominator
└─ “√(𝑎²− 𝑏²)” radical
├─ “⬚” degree
└─ “𝑎²− 𝑏²” radicand
└─ “−” text
├─ “𝑎²” superscript
│ ├─ “𝑎” base
│ └─ “2” script
└─ “𝑏²” superscript
├─ “𝑏” base
└─ “2” script
The semantic tree corresponds to Content MathML. It has drawbacks: 1) it’s bigger and requires more key strokes to navigate, 2) it doesn’t correspond to speech order, and 3) it requires a Polish-prefix mentality. Some people have developed such a mentality, perhaps having used HP calculators, and prefer it. But it’s definitely an acquired taste and it doesn’t correspond to the way that mathematics is conventionally displayed, edited, and spoken. Accordingly the first kind of tree seems significantly better for speech and editing, at least for the math encountered in grades K-12.
The choice for higher-level math is complicated by the fact that the usual meanings for superscripts, vertical bars, and other notation may be incorrect. For example, exponents are usually powers and it’s appropriate to speak 𝑎² as “a squared”. But in tensor analysis, exponents can be indices and saying them as powers is incorrect. One way around this is to say 𝑎² as “a superscript 2” or “a sup 2”, but it would be better to know the author’s intent and generate more descriptive speech. Another example is |𝑥|. In math up through calculus, this is the absolute value of 𝑥. However, in higher-level math it could mean the cardinality of the set 𝑥, or something else. In these cases and many others in advanced math, the semantic tree might reveal the author’s intent better than the display tree.
The MathML working group is studying ways to make Presentation MathML support accurate speech for ambiguous mathematical notations.
Both kinds of trees include nodes defined by the OMML entities listed in the following table along with the corresponding MathML entities
| Built-up Office Math Object | OMML tag | MathML |
| Accent | acc | mover/munder |
| Bar | bar | mover/munder |
| Box | box | menclose (approx) |
| BoxedFormula | borderBox | menclose |
| Delimiters | d | mfenced or mrow with mo’s |
| EquationArray | eqArr | mtable (with alignment groups) |
| Fraction | f | mfrac |
| FunctionApply | func | mrow with &FunctionApply; |
| LeftSubSup | sPre | mmultiscripts (special case of) |
| LowerLimit | limLow | munder |
| Matrix | m | mtable |
| Nary | nary | mrow followed by msubsup w n-ary mo |
| Phantom | phant | mphantom and/or mpadded |
| Radical | rad | msqrt/mroot |
| GroupChar | groupChr | mover/munder |
| Subscript | sSub | msub |
| SubSup | sSubSup | msubsup |
| Superscript | sSup | msup |
| UpperLimit | limUpp | mover |
| Ordinary text | r | mtext |
MathML has additional nodes, some of which involve infix parsing to recognize, e.g., integrals. The OMML entities were defined for typographic reasons since they require special display handling. Interestingly the OMML entities also include useful semantics, such as identifying integrals and trigonometric functions without special parsing.
In summary, math zones can be made accessible using display trees for which the node contents are spoken in the localized linear format and navigation is accomplished using simple arrow keys, Ctrl arrow keys, and the Home and End keys, or their Braille equivalents. Arriving at any particular insertion point, the user can hear or feel the math text and can edit the text in standard ways.

 Light
Light Dark
Dark
0 comments