Shorter quantum circuits

Vadym Kliuchnikov

February 4th, 20230 5

To solve some of the world’s most challenging problems in chemistry and materials science will require scaling up a quantum computer to a million qubits and beyond [BMTS+ 2022].

Microsoft has taken a more challenging, but what we believe to be a more promising path towards scaled quantum computing and designed our machine using topological qubits. Our unique qubit architecture is theorized to enable our quantum machine to be small enough to fit in a closet, fast enough to solve problems in a practical timeframe, and have the capability to control more than one million qubits. We are confident in this design given our significant physics breakthrough, which cleared a major hurdle toward engineering the world’s first topological qubit and ultimately, a scaled quantum machine. Anyone can access the same data as our scientists to better understand Microsoft’s approach to building a scalable, full-stack quantum machine.

In preparation for scaled quantum computing, Microsoft aims to empower developers with the knowledge and tools required to design impactful quantum applications. Understanding how many qubits are needed and how fast and reliable the quantum computer must be for practical applications is important for accelerating toward its scaled realization. At Microsoft, we’ve studied the resources required to unlock quantum advantage and focused on breakthroughs to deliver it sooner. Some of our breakthroughs were presented in Ghent, Belgium, at Quantum Information Processing 2023, which is one of the leading scientific conferences in the field. Together with our collaborators we presented results including:

The recordings of the talks are now available on YouTube, courtesy of QIP organizing committee:

This last result, described in our scientific paper “Shorter quantum circuits”, introduces methods to reduce the resources required to execute a very common set of operations in large-scale quantum algorithms called diagonal qubit rotation gates, with on average a 50% cost improvement. The runtime can be sped up by a factor of 2.5 by trading for a space (number of qubits) increase by the same factor. Our methods lead to an overall reduction in resources needed to run the algorithm’s instance.

You can try it for yourself! We have published an Azure Quantum Sample Notebook and a dataset that includes examples of circuits produced using the new compilation methods. It includes data analyses that reproduce the results detailed in the scientific paper and are used within the Microsoft Azure Quantum Resource Estimator.

The Resource Estimator is a software tool designed to help quantum algorithm designers and hardware engineers alike assess the resources required to run an instance of a quantum algorithm on fault-tolerant quantum computers. The methodology used by this tool is described in our programs’ recent resource estimation study, “Assessing requirements to scale to practical quantum advantage“, posted on the arXiv. Two of the scientists behind this work, Michael Beverland and Mathias Soeken, shared more about the tool and methodology on Wednesday February 8 during the QIP 2023 industry session.

Shorter-quantum-circuits-azure-notebook-sample

To access the notebook, follow the steps in Azure Quantum Notebooks tutorial

Let’s walk through the following steps to understand how the methods work:

Diagonal qubit rotation gates and where to find them

The diagonal qubit rotation gate is a one-qubit operation defined by the matrix:

Image rz theta

The standard instruction set for a fault-tolerant quantum computer, Clifford and T, only includes diagonal rotation gates for angles π/2, π/4, and π/8. However, many quantum algorithms require rotation gates with different angles.

For example, the Quantum Fourier Transform used in the factoring algorithm, requires rotation angles of π/2ᵏ for k = 4, 5, 6, …. The number of diagonal qubit rotation gates required for specific large-scale quantum algorithms can be found in the resource estimation study . For instance, the quantum dynamics problem in this study requires 3.01×10⁵ diagonal qubit rotation gates outside of the instruction set, the quantum chemistry algorithm requires 2.06×10⁸ such gates, and the instance of the RSA factoring challenge for a 2048-bit number requires 12 rotation gates outside of the instruction set.

So how do we map these different rotation gates to the instruction set available in the quantum computer? It turns out rotation gates outside of the standard instruction set can be approximated using circuits made up of a sequence of gates from the fault-tolerant instruction set. We call them “rotation circuits”. The question now becomes how to determine the approximation accuracy needed. Let me briefly explain.

Accuracy requirements: where do they come from?

To understand the accuracy requirement for individual diagonal qubit rotation gates, let us briefly discuss the accuracy requirements for quantum algorithms. Like probabilistic classical algorithms, quantum algorithms do not need to be perfectly accurate. A certain level of inaccuracy in the results produced by the quantum computer can be overcome through classical post-processing of the algorithm results. The algorithm designer typically specifies the required accuracy for the specific algorithm instance.

For instance, the quantum dynamics, quantum chemistry, and factoring examples mentioned earlier have tolerable levels of inaccuracy of 0.001, 0.01, and 1/3, respectively. There are several sources of inaccuracy, including failures of the instructions executed by the fault-tolerant quantum computer. It is common to divide the overall inaccuracy among various sources, such as dividing the overall inaccuracy of 0.001 into 0.0005 due to failures of the fault-tolerant instructions and 0.0005 due to imprecision of diagonal rotations. For 3.01×10⁵ diagonal qubit rotations, the inaccuracy per rotation would be split equally, resulting in an inaccuracy of 1.66×10⁻⁹.

The accuracy with which a quantum circuit over the fault-tolerant gate set approximates a given rotation is measured using the diamond norm. The action of any quantum circuit can be described by a quantum channel, and the diamond norm is a convenient way of measuring the difference between channels; the diamond norm fully captures the difference in the channels’ behavior. To learn more about the diamond norm and its use in this context, see Appendix B in “Shorter quantum circuits”. The higher the accuracy per rotation needed, the larger the contribution of the rotation circuits to the overall space and time cost of the quantum algorithm instance. In other words, better accuracy results in bigger and slower circuits. In the next section, we will discuss the contributions of the rotation circuits to the space and time costs in more detail.

Cost metrics: T count and T rate

Understanding the cost of a quantum algorithm is crucial in determining its feasibility and optimizing its performance. The two main contributors to the cost are the space-time cost of fault-tolerant Clifford operations and the space-time cost of T-state distillation.

T-states, which enable a non-Clifford fault-tolerant instruction called the T gate (that is Rz(π/8)), are essential for making a fault-tolerant quantum computer more powerful than a classical supercomputer. However, the cost of preparing one logical T-state is typically much higher than that of a logical Clifford operation.

The number of T-states used by a rotation circuit, as well as its T-state rate (number of T states used by the circuit per second), are good indicators of its overall space-time cost contribution. In our paper we compare two compilation methods, using Clifford+𝑇 and Clifford+√T gate sets. Note that for both gate sets, only Clifford operations and T-state preparations are used. The Clifford+√T gate set uses √T (that is Rz(π/16)) and √T³ (that is Rz(3π/16)) during an intermediate compilation step. The Clifford+√T method produces shorter quantum circuits with a higher T-state rate, making it a better option if faster execution is desired but with a higher cost in terms of physical qubits used.

Cost improvements

Before our work, there were three popular approaches for approximating rotation gates using a combination of Clifford and T gates with few qubits and without using resource states: Diagonal Approximation [RS2014], Fallback Approximation [BRS2014], and Mixed Diagonal Approximation [C2016],[H2016].

Diagonal approximation circuit

The Diagonal Approximation approach involves approximating a rotation gate with a sequence of one qubit Clifford and T gates.

Fallback approximation circuit

The Fallback Approximation uses two qubits and a measurement. It starts by trying to approximate the rotation gate with a shorter sequence of Clifford and T gates, and then falls back to the diagonal approximation if necessary.

Image mixed diagonal approximationMixed diagonal approximation circuit

The Mixed Diagonal Approximation involves randomly applying one of several diagonal approximations with carefully chosen probabilities to achieve better accuracy.

In our work, “Shorter quantum circuits”, we improve the fallback approximation approach by allowing the success probability of the first step to be selected ahead of time. We also combine the mixing techniques with the fallback approximation. The plot and table below show the cost improvements for the Clifford and T gate set for a dataset of random angles. The results show that our mixed fallback approach has the best T count linear fit, as a function of diamond norm accuracy ε.

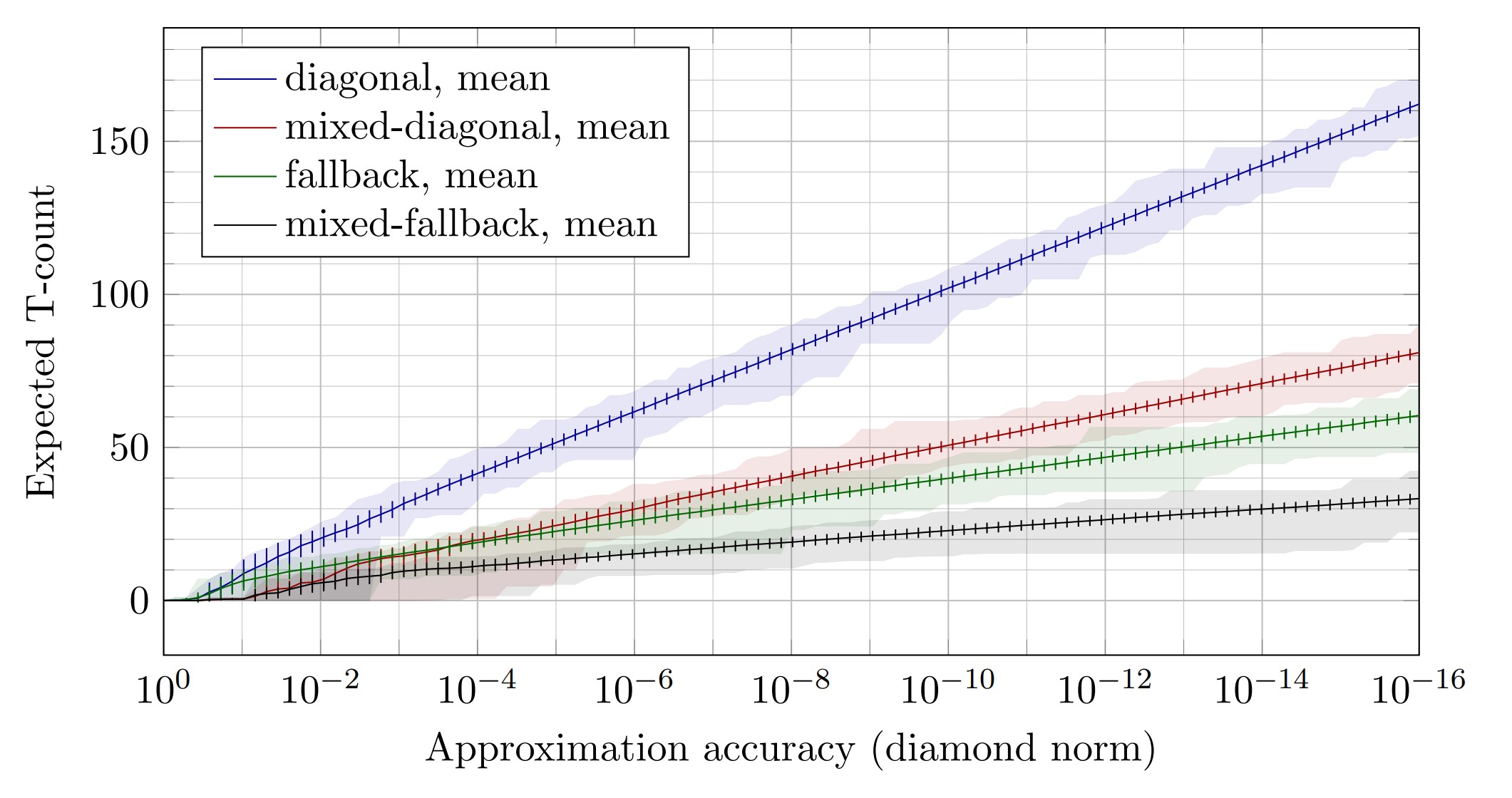
expected-t-count

Expected T count as a function of approximation accuracy using Clifford and T gate set

Approximation approach T count linear fit
Diagonal [RS2014] 3.02 log₂(1/ε) + 1.77
Fallback [BRS2014] 1.03 log₂(1/ε) + 5.75
Mixed diagonal [C2016],[H2016] 1.52 log₂(1/ε) – 0.01
Mixed fallback [Shorter Quantum Circuits] 0.53 log₂(1/ε) + 4.86

We also extend all the above approaches to the Clifford+√T gate set. The rotation circuit produced using this gate set has a T rate that is 2.5 times higher but has a similar T count. Additionally, we present a unified approach across all approximation approaches and gate sets with various small improvements over previous work.

High-level overview of the compilation methods

Our unified compilation approach, like previous works [RS2014], [KBRY2015], consists of three steps:

  1. Identifying an integer point within a region in Euclidean space.
  2. Finding a unitary that can be exactly represented using a sequence of gates from the chosen gate set (either Clifford and 𝑇 or Clifford and √T) by solving a system of polynomial equations with integer variables related to the integer point from step 1.
  3. Decomposing the exactly representable unitary into a sequence of gates from the chosen gate set using exact synthesis algorithms.

The first step determines the region based on the desired approximation accuracy, T count, and gate set. We provide methods for constructing a suitable region for each approximation approach. For the Clifford and 𝑇 gate set, the region is four-dimensional, while for the Clifford and √T gate set, the region is eight-dimensional. In practice, we use integer programming with convex constraints for the convex hull of the region.

In the second step, the system of polynomial equations is reduced to a relative norm equation problem in a number field related to the chosen gate set. Solving the norm equation involves integer factoring, but in practice, we encounter instances that are easy to factor.

The third step utilizes exact synthesis algorithms that take advantage of the fact that the cost of unitary operations exactly representable using either the Clifford and 𝑇 or Clifford and √T gate sets can be calculated quickly without knowledge of the gate sequence. The exact synthesis algorithm decomposes the unitary by multiplying it with the gates from the gate set and reducing the cost greedily. It is like solving a combination lock by trying each digit until you find the correct one. In our case, the lock clicks when each correct digit is found. The number of digits represents the number of non-Clifford gates in the sequence.

This approach can be applied to many other gate sets that allow for a certain number theoretic description as described in [KBRY2015]. A particularly simple gate set known as the V basis results in a two-dimensional region in step 1, shown below, and a simple equation of x²+y²=c in integer variables x and y in step 2, instead of a system of four or eight equations for the Clifford and 𝑇 or Clifford and √T gate sets.

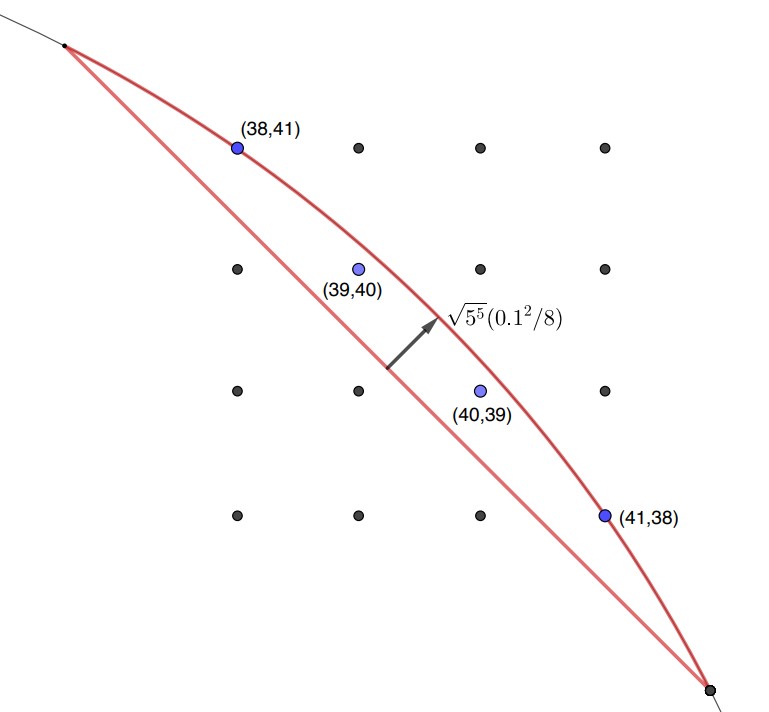
v gates region

A region for diagonal approximation approach when using V basis gate set

Beyond diagonal gates: magnitude approximation problem

The examples of quantum algorithms we have discussed above use Clifford operations, Toffoli gates and diagonal qubit rotation gates. However, an algorithm designer may want to use arbitrary one-qubit gates, one-qubit state preparations, or two-qubit gates, which are currently reduced to Clifford and diagonal qubit gates through fault-tolerant compilation.

To address this, we introduce the magnitude approximation problem, which helps reduce the cost of compiling arbitrary one-qubit and multiple-qubit gates. This problem also has a mixed version and is covered by our unified compilation approach.

The dataset and the notebook

To enable trying the methods for yourself, we present a dataset that contains quantum circuits approximating diagonal qubit rotation gates using four approximation methods: diagonal, fallback, mixed diagonal, and mixed fallback. The gate sets used in the circuits include both Clifford and 𝑇 and Clifford and √T. The target rotation angles in the dataset consist of a thousand random angles and angles used in the Quantum Fourier Transform.

Shorter Quantum Circuit Sample

To access the notebook, follow the steps in Azure Quantum Notebooks tutorial

A Jupyter notebook is available on GitHub and as part of the Azure Quantum Sample Notebooks that explains the structure of the dataset and demonstrates how to reproduce the results from the study. The notebook and dataset provide opportunities for reproducing our results, comparing future approaches to our methods, and conducting more in-depth analysis.

With the dataset, you can answer questions such as what the T-count distribution of fallback circuits looks like or which gates are used by the approximation protocols. Additionally, if you have your own cost metric, you can use the dataset to evaluate our circuits.

Do not miss the chance to explore the exciting world of quantum circuits and improve your understanding of diagonal qubit rotation gates! Take advantage of our dataset, Jupyter notebook, and Azure Quantum Sample Notebooks to compare and analyze the results from the four approximation methods and two gate sets. Try your own cost metric evaluation and unlock new insights in quantum circuit design. While you are at it, try out other Azure Quantum Resource Estimation notebooks and join us on the path to accelerate quantum advantage.

 

Vadym Kliuchnikov

Read next

0 comments

Discussion is closed.

Feedback usabilla icon