Quantum developer tools for chemistry
Co-authored by Hongbin Liu, Researcher at Microsoft Quantum
Quantum computers will be able to reveal the exact quantum nature of chemical systems exponentially faster than classical computers. That’s why one of the most impactful future applications of quantum computing is chemistry simulation. Quantum mechanics plays a dominant role in the behavior of molecular systems at the fundamental scales. However, the complex nature of quantum effects make them computationally expensive to simulate. For instance, a simple, approximate quantum chemistry calculation could take many hours to run on a large computational cluster. While exact calculations may even be intractable for these classical systems, quantum computers can reveal the exact quantum nature of chemical systems. Such advantage can unlock the ability to study molecules and chemical phenomena we were not able to study before. If you are interested in what chemical systems can benefit most from quantum computers, please take a look at our latest work: Prospects of Quantum Computing for Molecular Sciences.
To get started with quantum development of chemistry algorithms, you can either run quantum algorithms on a simulator or on near-term hardware. Simulators can be a great way to get started with quantum programming, and they also offer a way to understand the hardware requirements of a specific algorithm. The Microsoft Quantum Development Kit (QDK) offers multiple simulator back-ends that can be targeted by the Q# compiler and runtime. In addition, we offer Python-based tools that easily let you plug in your favorite libraries to analyze and plot the results. Many of the chemistry tools in the QDK have resulted from work done by our research team in collaboration with the Advanced Computing, Mathematics, and Data Division at Pacific Northwest National Laboratory (PNNL). Some of our tools include interacting with the Microsoft Quantum Editor on EMSL Arrows, a computational chemistry tool built and maintained by the PNNL team. In this post we will show examples of chemistry algorithms that you can run with the QDK and the Q# Chemistry library.
Simulating the molecular ground state
Energy is one of the most important properties of a molecule from the computational perspective. It can be directly translated to metrics and design principles to guide real-world application, for instance the design of catalysts or photovoltaic materials. As most of the time molecules are in their ground state, i.e. lowest energy state, the evaluation of ground state energy thus becomes the most fundamental step to understand the molecule. A scalable and powerful algorithm that can be used to calculate the ground state is called Quantum Phase Estimation (QPE). QPE projects the quantum state onto an eigen state of the Hamiltonian of the molecule, such that it always produces exact energies. Here we will demonstrate how to run Robust Phase Estimation, a version of Quantum Phase Estimation algorithm that uses fewer qubits, using the QDK developer tools for chemistry. This calculation consists roughly of the following steps:
- Compute the electron interactions (i.e. Hamiltonian terms) using chemistry simulation packages such as NWChem.
- From the results in (1), generate the coefficients for generating a good guess of the ground state, also known as a trial state, to encode in qubits. Optionally, it is possible here to perform further calculations in chemistry packages to get an elaborate trial state if higher accuracy is required in the estimation.
- Apply Robust Phase Estimation algorithm to estimate the phase of the trial state. This prepares the trial state generated in (2) and projects the state onto a possible ground state of the Hamiltonian.
- Repeat (3) and post-select to find the solution that provides the lowest energy.
In the example below, we will run a Q# program that runs Robust Phase Estimation on a simulator, in particular, the Q# full state simulator. The Q# program is defined in a Q# file and contains an operation that we can import and run from a Q# entry point, the IQ# kernel, a host program in C# or Python, or directly from a Jupyter notebook, as we will do in this blog post.
namespace Microsoft.Quantum.Chemistry.Trotterization {
open Microsoft.Quantum.Core;
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Canon;
open Microsoft.Quantum.Chemistry;
open Microsoft.Quantum.Chemistry.JordanWigner;
open Microsoft.Quantum.Simulation;
open Microsoft.Quantum.Characterization;
open Microsoft.Quantum.Convert;
open Microsoft.Quantum.Math;
operation GetEnergyRPE (
JWEncodedData: JordanWignerEncodingData,
nBitsPrecision : Int,
trotterStepSize : Double,
trotterOrder : Int
) : (Double, Double) {
let (nSpinOrbitals, fermionTermData, inputState, energyOffset) = JWEncodedData!;
let (nQubits, (rescaleFactor, oracle)) = TrotterStepOracle(JWEncodedData, trotterStepSize, trotterOrder);
let statePrep = PrepareTrialState(inputState, _);
let phaseEstAlgorithm = RobustPhaseEstimation(nBitsPrecision, _, _);
let estPhase = EstimateEnergy(nQubits, statePrep, oracle, phaseEstAlgorithm);
let estEnergy = estPhase * rescaleFactor + energyOffset;
return (estPhase, estEnergy);
}
}
This operation makes use of the Q# Libraries, in particular the Quantum Chemistry Library, and will return a tuple of the estimated phase and energy of the ground state of the molecule. For more information on the above libraries and operations used in this sample, please take a look at the extensive Q# user guide.
Robust Phase Estimation example: caffeine
To start off calculating the ground state, we need to first load the molecule such that we can construct its electronic model. Here, we will use an XYZ file, which specifies the spatial coordinates of the atoms in the molecule. To inspect the molecule, we can use the qdk Python package and visualize it in Jupyter notebook. To install the qdk package and its dependencies, we recommend installing conda and running:
$ conda install -c rdkit rdkit $ pip install qdk
If you don’t have it already, make sure to also install the qsharp package:
$ conda install –c quantum-engineering qsharp
Now, start a Jupyter notebook by running:
$ jupyter notebook
This opens a new browser window with a Jupyter server, from which you can start a new notebook with a Python kernel. To load the molecule inside the notebook, simply import the Molecule class and use the from_xyz class method to create an instance:
In: from qdk.chemistry import Molecule
caffeine = Molecule.from_xyz("data/xyz/caffeine.xyz")
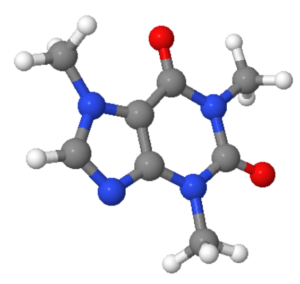
caffeine
Out:

This returns an interactive JSMol widget in the notebook.
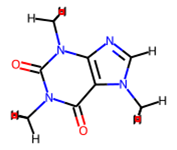
For a static image of the molecule generated by RDKit, run:
In: caffeine.mol Out:
We can then inspect how many electrons this molecule has:
In: caffeine.num_electrons Out: 102
And the atomic number of its atoms:
In: caffeine.atoms Out: [1, 6, 7, 8]
To evaluate the energy of a molecule, we need to choose a set of one-electron basis functions (often known as orbitals) to represent the electronic wave functions. Here, we use one of the most elementary basis sets, STO-3G, to represent the caffeine molecule:
In: caffeine.num_orbitals(basis="STO-3G") Out: 80
In total, there are 80 spatial orbitals. The state of an orbital, which can contain up to two electrons, can be represented by 2 qubits. One can easily see that the classical simulation of many orbitals is very costly due to the exponential complexity of simulating qubits. Luckily, only a couple of frontier orbitals (in many cases, the highest-occupied-molecular-orbital, HOMOs; and lowest-unoccupied-molecular-orbital, LUMOs) dominate the chemical properties of the molecule. We only need to probe the molecule’s quantum properties within those chemically most relevant orbitals, also known as active space, and use approximations to estimate the energy contribution of rest of the orbitals. This largely reduces the number of orbitals we need to map to the qubits.
For this problem, we can start off with four active orbitals, which means we will need 8 qubits to encode the problem. RPE also requires one auxiliary qubit, which would bring us to 9 qubits in total, which is a number we can comfortably simulate on a laptop. To do that, we need to calculate the electronic properties using a computation chemistry tool such as NWChem or OpenMolcas. To use NWChem in the browser and generate a Broombridge file directly, use the Microsoft Quantum Editor on EMSL Arrows.
To encode the electronic properties, also known as the electrionic Hamiltonian, we need to store them in a file format using the Broombridge Quantum Chemistry Schema. You can use the following Python code to load it via the QDK Python package:
In: from qdk.chemistry.broombridge import load_and_encode
encoded_data_caffeine = load_and_encode("data/broombridge/caffeine.yaml")
Then we can import and call the Q# operation from Python:
In: from Microsoft.Quantum.Chemistry.RPE import GetEnergyRPE
GetEnergyRPE.simulate(
JWEncodedData=encoded_data_caffeine,
nBitsPrecision=10,
trotterStepSize=0.2,
trotterOrder=1
)
Out: (-0.3383813350711708, -627.6309264967134)
By classical simulations we found the exact ground state energy to be -627.63095945558848 Ha. Given that we are using 10 bits of precision with a step size of 0.2, we expect an error of (1/210)/0.2=4*10-3, which is 4 mHa accuracy, so our result from RPE is within the expected error range.
To see how resource intensive this calculation was, we can use the estimate_resources method:
In: GetEnergyRPE.estimate_resources(
JWEncodedData=encoded_data_caffeine,
nBitsPrecision=10,
trotterStepSize=0.2,
trotterOrder=1
)
This will calculate the resources and return a Python dictionary:
Out: {
'CNOT': 42913920,
'QubitClifford': 24522844,
'R': 9196140,
'Measure': 609,
'T': 0,
'Depth': 0,
'Width': 9,
'QubitCount': 9,
'BorrowedWidth': 0
}
Here, the values in the dictionary return the estimates of numbers of different gates and circuit depth required to run this algorithm. To learn more about what each of these metrics represent, please visit the “Metrics reported” section of the docs of the Q# resources estimator simulator back-end.
Based on the resource metrics, it looks like simulating the ground state of caffeine using RPE requires quite a lot of resources. We need many millions of CNOT gates! Obviously, this is not yet realistic on near-term hardware, such as the systems available on Azure Quantum. So how are we going to simulate a chemistry molecule on a near-term machine? For this purpose, variational methods might come in handy.
Variational Quantum Eigensolver
While Quantum Phase Estimation algorithms such as the RPE sample mentioned above provide an exact solution, there are variational methods in chemistry that are used to iteratively get to an approximate solution. We can do exactly that using small and shallow quantum algorithms such as the Variational Quantum Eigensolver. The VQE algorithm starts with a parameterized trial state, and optimizes the parameters to approximate the ground state energy. The protocol is as follows:
- Compute the electron interactions (i.e. Hamiltonian terms) using a chemistry simulation package.
- From the results in (1), generat a good guess of the ground state (trial state), and encode it in qubits.
- Estimate the energy of the trial state by doing a projective measurement for each term in the Hamiltonian.
- Modify the trial state using its parametric definition.
- Repeat steps 2 to 4 until the energy of the molecule is minimized.
The algorithm requires many evaluations on quantum hardware, but this will give us an approximation of the ground state. The Q# program that implements VQE uses the EstimateEnergy operation which uses EstimateFrequencyA to estimate the fraction of samples of a projected measurement that are in the Zero state. This operation is run using a built-in emulation feature in the simulator that uses binomial sampling to simulate running multiple shots on quantum hardware without directly inspecting the quantum state, which allows us to run the VQE algorithm on millions of shots without any significant added run time. Note that on real hardware, this emulation is not possible, so it would take a significantly longer time to run.
The Q# program is shown below. The operation takes the Hamiltonian information, then encodes the wave function ansatz as a linear combination of the Hartree-Fock state, two singly excited states, and a doubly excited state. VQE modifies the input state with the given parameters theta1, theta2 and theta3, and returns the estimated ground state energy for that given input state, in order to determine the variational bound of energy.
namespace Microsoft.Quantum.Chemistry.VQE {
open Microsoft.Quantum.Core;
open Microsoft.Quantum.Chemistry;
open Microsoft.Quantum.Chemistry.JordanWigner;
open Microsoft.Quantum.Chemistry.JordanWigner.VQE;
open Microsoft.Quantum.Intrinsic;
operation GetEnergyVQE (JWEncodedData: JordanWignerEncodingData, theta1: Double, theta2: Double, theta3: Double, nSamples: Int) : Double {
let (nSpinOrbitals, fermionTermData, inputState, energyOffset) = JWEncodedData!;
let (stateType, JWInputStates) = inputState;
let inputStateParam = (
stateType,
[
JordanWignerInputState((theta1, 0.0), [2, 0]), // singly-excited state
JordanWignerInputState((theta2, 0.0), [3, 1]), // singly-excited state
JordanWignerInputState((theta3, 0.0), [2, 3, 1, 0]), // doubly-excited state
JWInputStates[0] // Hartree-Fock state from Broombridge file
]
);
let JWEncodedDataParam = JordanWignerEncodingData(
nSpinOrbitals, fermionTermData, inputState, energyOffset
);
return EstimateEnergy(
JWEncodedDataParam, nSamples
);
}
}
To compare this approach to the previous calculation of caffeine using RPE, we can estimate how many resources it will take to run this algorithm. Because it’s variational, let’s look at just the cost for one iteration (nSamples=1):
In: from Microsoft.Quantum.Chemistry.VQE import GetEnergyVQE
GetEnergyVQE.estimate_resources(
JWEncodedData=encoded_data_caffeine,
theta1=0.001,
theta2=-0.001,
theta3=0.001,
nSamples=1
)
Out: {
'CNOT': 0,
'QubitClifford': 1440,
'R': 0,
'Measure': 3240,
'T': 0,
'Depth': 0,
'Width': 8,
'QubitCount': 8,
'BorrowedWidth': 0
}
Note that while the resources for a single run are much lower compared to RPE, this algorithm has a much higher total cost because we still need to multiply the numbers for gates and measurements above by the number of samples and optimization steps, as discussed in our recent prospects.
Let’s try out calculating the energy for a given trial state of the ground state of caffeine for a given initial set of parameters theta1, theta2 and theta3:
In: GetEnergyVQE.simulate(
JWEncodedData=encoded_data_caffeine,
theta1=0.001,
theta2=-0.001,
theta3=0.001,
nSamples=10000000
)
Out: -627.6287520087537
To find the ground state energy, we need find the optimal values of theta1, theta2 and theta3 at which the energy is minimized. Instead of doing a large scan over the entire parameter space, we run this quantum simulation using an optimizer. For that, we can use any optimization function that can minimize a cost function given a set of input parameters. Here, we will use scipy.optimize:
from scipy.optimize import minimize
def run_program(var_params, num_samples) -> float:
# run parameterized quantum program for VQE algorithm
theta1, theta2, theta3 = var_params
return GetEnergyVQE.simulate(
JWEncodedData=encoded_data_caffeine,
theta1=theta1,
theta2=theta2,
theta3=theta3,
nSamples=num_samples
)
def VQE(initial_var_params, num_samples):
""" Run VQE Optimization to find the optimal energy and the associated variational parameters """
opt_result = minimize(
run_program,
initial_var_params,
args=(num_samples,),
method="COBYLA",
tol=0.000001,
options={'disp': True, 'maxiter': 200,'rhobeg' : 0.05}
)
if opt_result.success:
print(opt_result.message)
print(f"Result: {opt_result.fun} Ha")
print(f"Number of evaluations: {opt_result.nfev}")
print(f"Optimal parameters found: {opt_result.x}")
return opt_result
We can then run this to find the ground state energy. To get an accurate result, let’s use 10 million samples:
In: VQE([0.001, -0.001, 0.001], 10000000) Optimization terminated successfully. Result: -627.6287829908172 Ha Number of evaluations: 39 Optimal parameters found: [ 0.05093427 -0.00092959 0.05098581]
This prints the and returns the optimization result returned by the optimizer. For a more detailed overview of the parameters that are returned by the minimize function, see the scipy.optimize documentation page.
Important to note here is that the energy estimate by VQE is not going to be as close to the exact energy that we simulated earlier with the RPE sample. This is mainly because we chose a fairly simple trial state. By choosing a more elaborate trial state we will be able to get a better estimate, but this would require us to use more qubits and gate operations in order to run the algorithm.
Getting started with Quantum Chemistry development in Q#
If this blog post has inspired you to develop quantum algorithms in Q#, we encourage you to get started with our MS Learn modules to get your machine set up to run quantum simulations on your own machine:
Create your first Q# program by using the Quantum Development Kit – Learn | Microsoft Docs
To get a refresher of the fundamental concepts of quantum computing, this MS Learn learning path might help you get started as well:
Quantum computing foundations – Learn | Microsoft Docs
If you prefer to get started with some hands-on samples that you can run directly including the one covered in this blog post, we recommend cloning our Quantum repo which contains more chemistry examples than the ones just mentioned in this blog post:
microsoft/Quantum: Microsoft Quantum Development Kit Samples (github.com)
Alternatively, launch the repo in Binder to can get started running algorithms via IQ# right away:
The Broombridge files and example code that were used in this blog post are part of the qdk-python repo:
microsoft/qdk-python: Python packages for the Microsoft Quantum Development Kit (QDK) (github.com)
If you have any questions, please don’t hesitate to get in touch with us and other quantum developers using the comments to this blog post or the Q# community. Happy quantum developing!

 Light
Light Dark
Dark
0 comments